Question
Three females and three males are applying for three identical positions with a company. The hiring committee wants to hire at least one woman. How many different ways can the four positions be filled?
Student answer
Since at least one woman will be hired, choose 1 woman out of 3 firstly to secure a woman C(3,1). Secondly, choose the other two candidates from the other five persons, including 2 females and 3 males, C(5,2). Multiplying C(3,1) and C(5,2) leads to an answer of 30 ways.
I. What’s the logic mistake?
At a first glance, the logic offered by the student seems to be reasonable. Selecting one woman at the first step surely can gaurantee that at least one woman will be hired. Unfortunately, the answer is wrong, not even close to the correct one. Can you identify the logic mistake?
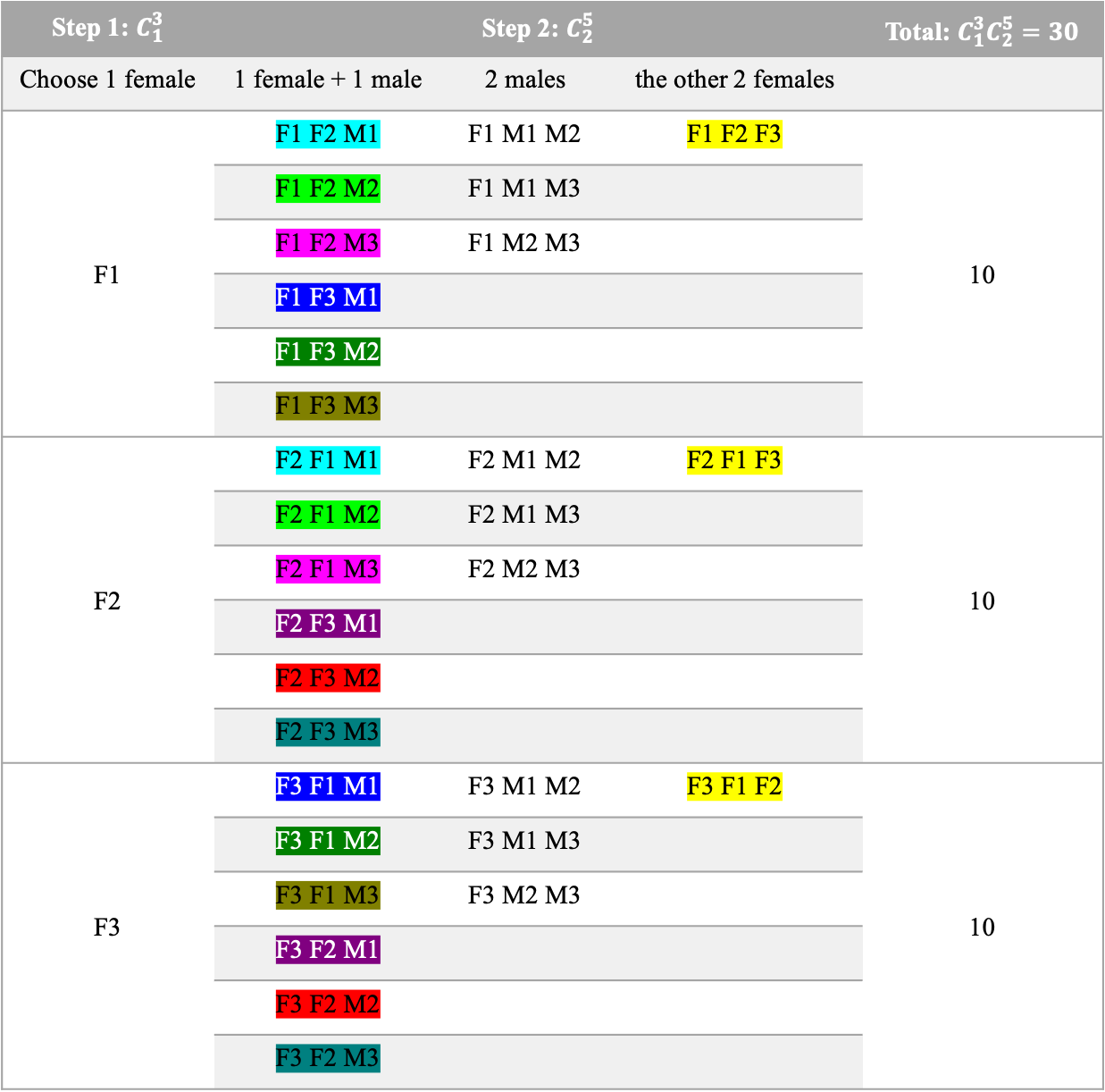
The most straightforward way to identify the problem is through a tree diagram. As shown in the table, F1, F2, and F3 represent three females, there are three ways to choose 1 female out of 3 females. In step 2, there are three distinct cases to choose 2 persons out of the other 5 persons: 1 female and 1 male, 2 males, and 2 females. Different colors are used to identify the repeated combinations in the table. Exactly, there are 9 colors representing 9 repeated combinations when choosing 1 female and 1 male in step 2. Moreover, look at the column of choosing 2 females in step 2, all of them are the same. Why? There are 3 females and there’s only one way to choose 3 females out of 3 females: choose all of them.
Why are there repeated ones?
When steps are involved, you naturally introduce ‘ORDER’ to the problem. For example, F1 F2 M1 is the same combination as F2 F1 M1 even though they are in different orders. This is the mistake! In mathematics, it is called ‘OVERCOUNTING’. Only combination matters here. Permutation will lead to overcounting.
II. The correct logic
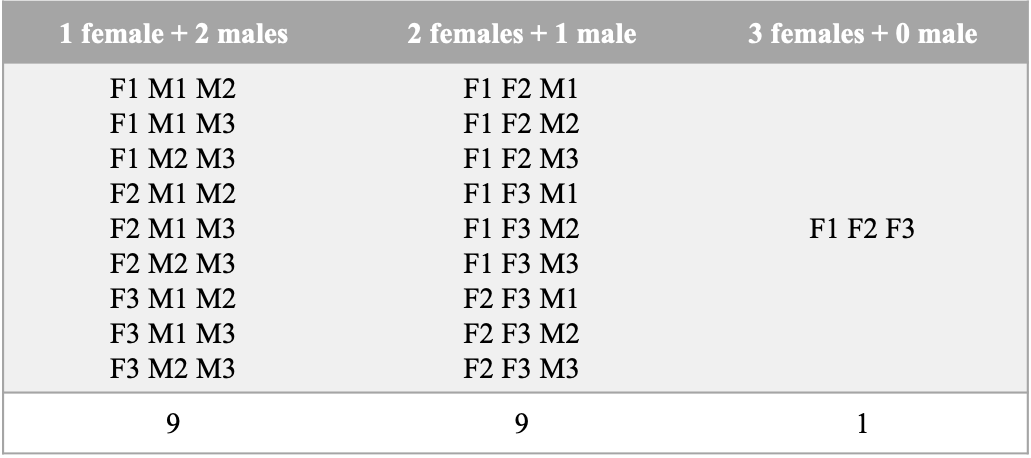
At least one woman indicates the following 3 cases:
> 1 female + 2 males: C(3,1)*C(3,2)=9
> 2 females + 1 male: C(3,2)*C(3,1)=9
> 3 females + 0 male: C(3,3)*C(3,0)=1
So, the problem can be solved by adding the combinations in three different cases:
9+9+1 = 19.
To clearly show the combinations, a table is used again below for your reference.
III. Alternative Strategy?
In general, ‘At least’ problems are better solved by the complement of this event. Event and the complement of the event form a complete whole.
*** Event + Complement of this event = Whole ***
Therefore, subtracting the complement of the event from the whole leaves the event, the desired answer.
What is the “WHOLE” of this problem?
choosing 3 candidates out of 6 people is the “WHOLE”: C(6,3)=20
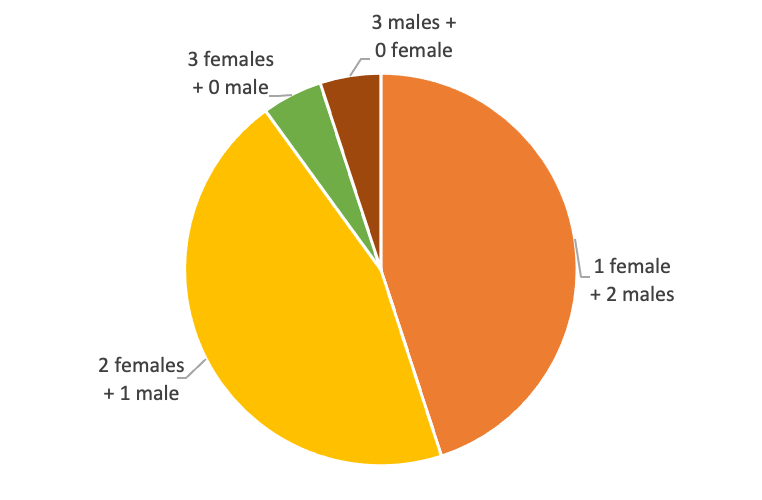
The “WHOLE” is actually composed of 4 distinct cases:
> 0 female + 3 males: C(3,0)*C(3,3)=1
> 1 female + 2 males: C(3,1)*C(3,2)=9
> 2 females + 1 male: C(3,2)*C(3,1)=9
> 3 femlaes + 0 male: C(3,3)*C(3,0)=1
Again, the WHOLE is 1+9+9+1=20 ways.
The event in the problem is “At least one woman”. So, the complement of this event is “no woman”:
0 female + 3 males: C(3,0)*C(3,3)=1
Answer : WHOLE — No woman = 20–1=19
Counting Techniques are all about logical thinking.
Leave a Reply