When we were having dinner, Shawn’s dad casually tested his calculation.
Dad: 1 plus 3 is?
Shawn: 4
Dad: How about 1 plus 3 plus 5?
Shawn: 9
Dad: Add the next odd number 7?
Shawn: Well, it is 9 plus 7, and it equals 16.

Shawn’s dad suddenly realized that square numbers could be formed by adding consecutive odd numbers together. Why is it so magical? We know that odd numbers form an arithmetic sequence, the sum can be easily obtained through the formula, and for this case, it is n squared. Shawn was curious about but confused with our conversation. Exactly, it is such an interesting mathematical relationship that can naturally trigger a young kid to explore further. However, to a kid in Grade One, explaining by algebraic expressions is like playing the piano to a cow (Chinese old saying). So, I used SQUAREs to visualize SQUARE Numbers.

I. Activate Prior Knowledge

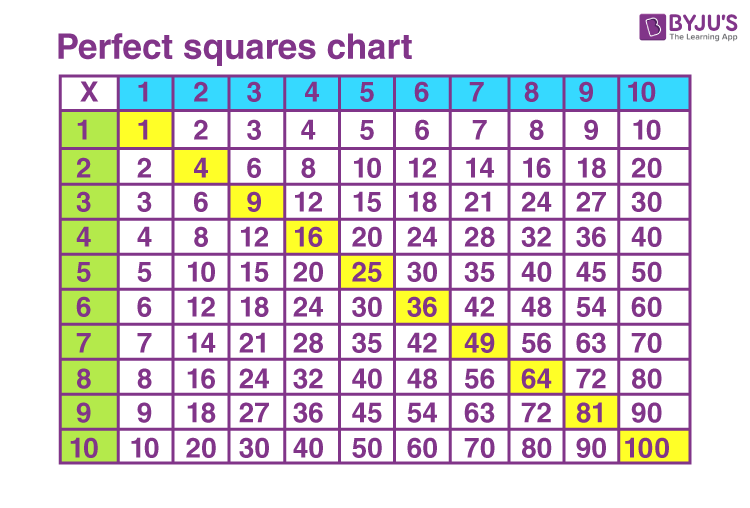
Shawn learned multiplication through drawing columns and rows. He’s really sick of remembering the multiplication table. How? He’d rather draw tables and repeatedly add the same number a certain amount of times. To some extent, thanks to his laziness, he has developed a sense of geometrical illustration to represent numbers and operations, which my generation didn’t have at his age. Given the multiplication table below, the highlighted numbers are the product of the same integers, such kinds of numbers are square numbers. Shawn quickly related square numbers to graphics: the same number of columns and rows, this is how a square is formed. Great, it is time to move forward.

II. Geometric Illustration

Lego, you are popular for a reason!
I used a square lego block to draw a yellow square first.
Me: Can you make a bigger square if I give you one more square?
Shawn: No, I need 4 squares to make a bigger square.
I then asked Shawn to draw the second square and color the extra three squares blue. This square is expressed as 2 times 2.

Me: How many square blocks are needed to form a third square?
Shawn tried to place more square blocks together and he used 9 blocks. He noticed that there are three columns and rows so that 3*3=9. The same as square 2*2, I asked Shawn to color the third one (Figure 2). 
Me: How many more square blocks are needed compared to the second one?
Shawn counted and replied, ‘5 more’.

Before moving on to the fourth square, I asked, ‘how many more square blocks are needed to form the fourth square?’ By asking this question, I was leading him to find the pattern of adding consecutive odd numbers. I’m too fast or aggressive here. For a pattern to be obvious to anyone, a minimum of three or four numbers are essential. Shawn repeated the steps in the squares 2*2 and 3*3 and found that 7 blocks were added to form a 4*4 square. He seems to be more interested in both drawing and calculating. Before I asked him to create the fifth square, he drew the 5*5 square by himself and grasped the pattern: 9 blocks should be added to the fourth square as a new layer to form the fifth one.

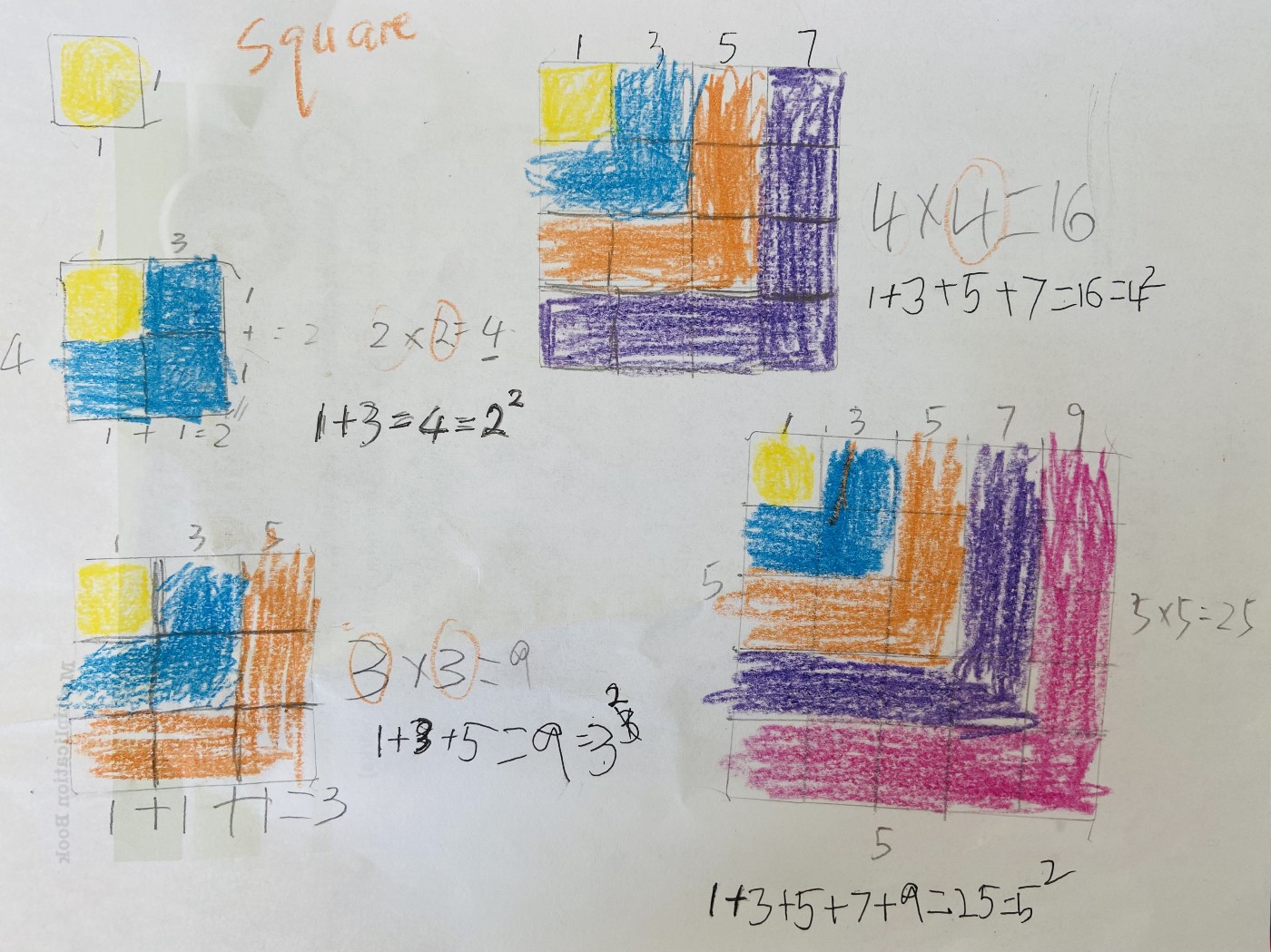
III. Discover the Patterns

In order for the pattern to be clearer, I marked 1, 3, 5, 7, and 9 on the correspondent layers shown by distinct colors. Take the 2*2 square as an example, 1 block surrounded by another 3 blocks is expressed as 1+3=4, and 4=2²
Me: Could you write down the expressions for the 3rd, 4th, and 5th squares following my example?
Shawn wrote 1+3+5=9=3³.

He doesn’t know square numbers and of course, he doesn’t know that 2*2 is abbreviated by 2². He wrote 3³ as he thought the 3 in the superscript means the second 3. I briefly explained that 3+3=3*2 showing the same number was added twice can be abbreviated by the number multiplied by 2. Similar to this, 3*3 shows that the same number is multiplied twice, which can be expressed by the number squared and this square is a 2 in the superscript. I don’t expect a 1st grader to truly understand exponents but planting a seed at an appropriate time is an art. 
He then correctly wrote 1+3+5+7=16=4² and 1+3+5+7+9=25=5²

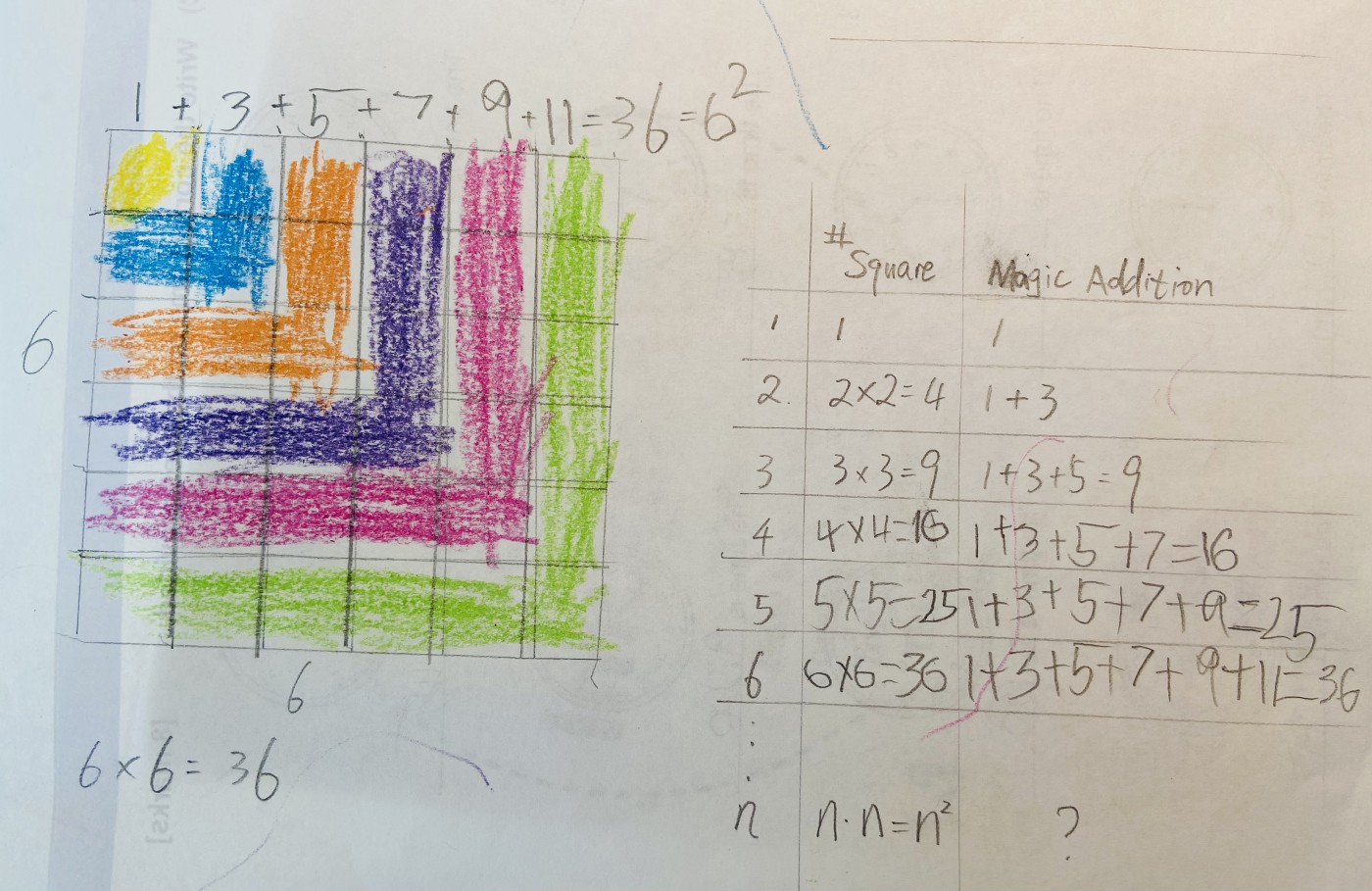
To sum up, he decided to draw a big square on a whole piece of paper. He did it all by himself, from drawing the squares, coloring each layer, adding the numbers, to writing the square number.

Instant Review
Making an immediate summary of what we’ve just learned is a good way to consolidate our understanding of the new discoveries. Shawn thought that he knew everything now and that I should record a video for him to share his new knowledge on youtube. We all know that knowing and teaching are basically two stories. I asked him what he learned from all of these illustrations and expressions. He replied, ‘squares and square numbers’. Should I be happy? The idea came from the addition of consecutive odd integers and it seemed that he doesn’t care about it that much. Well, at least he learned that square numbers were perfectly demonstrated by squares. To remind him of the key knowledge, I made a chart (Figure 3) to show:
1. the number of unit squares used to form the nth square is n*n=n².
2. a square number is the sum of the consecutive odd integers. 3² is obtained by adding the first three positive odd integers; 4² is the sum of the first four positive integers;

Arithmetic Sequence
How about the nth square? 
Why are there such magical relationships between square numbers and odd numbers?
It is where the formula of arithmetic series comes from. The arithmetic sequence is 1 + 3 + 5 +…+ 2n-1
Write it in the reversed order 2n-1+2n-3+2n-5+…+1
Add the two expressions 2n+2n+2n+…+2n
There are n ‘2n: n*2n=2n²
Since we add the same sequence twice, divide the above expression by 2: 2n²/2=n². 
Proved! Amazing, isn’t it?

Variables and arithmetic sequences are way beyond Shawn’s age. Again, planting a seed at an appropriate time.

IV. Turn 2D to 3D

Me: Shawn, you built a Lego pyramid last week, right?
Shawn: Yeah. Sister broke it but I can build a new one.
Me: How about we build all the 6 squares together?
Shawn: Is it a pyramid?
Me: You can find the answer by adding the 6 squares and I can help you.

We spend about 20 minutes building the 3d figure together (Figure 4). Is it a pyramid? It is not the traditional Egyptian pyramid but it is a special pyramid. 
On one hand, the process of building the pyramid is a favored tool to consolidate kids’ understanding of abstract numbers. 
On the other hand, how many unit squares in total are there in the pyramid? In other words, 1²+2²+3²+…+n²=?
Lego can help to reveal the mystery. This allows me to design the next topic for Shawn.