In the competitive exam-oriented educational system, it is common for Chinese students to dedicate their summer and winter breaks to advance their understanding of upcoming semester’s subject matter, aiming to maintain their advantageous position. Students who have already delved into algebra may enjoy certain benefits over their counterparts who have not done so. For instance, there are certain steps and strategies to solve equations, which guarantees that one can master the skills with diligent practice. In contrast, geometric proof, reliant on robust deductive reasoning rather than the adherence to routine formulas, present a greater degree of flexibility, challenge, and even occasional mystique. Does a head start in geometric proofs also yield advantages? More precisely, what role does such a head start play in cultivating the deductive reasoning abilities required for the cognitively demanding Chinese mathematics curriculum?

Students’ Deductive Reasoning Abilities
Low-Cognitive
Having been a math teacher for a decade, I would say that a head start in geometry does provide benefits, but confined to concepts and problems of low-cognitive complexity. Learning all the contents in a short time period is possible, but only at an entry level, far from the cognitive demands imposed by the Chinese mathematics curriculum. Annually, approximately half of the students in my honor math class preemptively engage with geometric proofs, including Jerry. Surely, the head start enables students such as Jerry to outperform their classmates who learn the contents for the first time in the upcoming semester. Those who have already mastered the three methodologies for prove congruent triangles can remember the theorems and directly apply them to establish congruence in varied scenarios. Quesiton 1 in Table 1 is a typical low-cognitive question in the Chinese mathematics curriculum, which requires only the knowledge of congruent triangles and equilateral triangles; moreover, the given conditions are adequate to straightforwardly deduce the congruence of triangle AOE and COE. Witnessing their newfound mathematical abilities and progress in contrast to their past performance, I used to be surprised and glad with them when I was a new teacher. However, the advantages of a head start dissipate quickly within the first month of the semester. This transition invariably transpires as the content escalates in complexity, exemplified by Question 2 in Table 1.

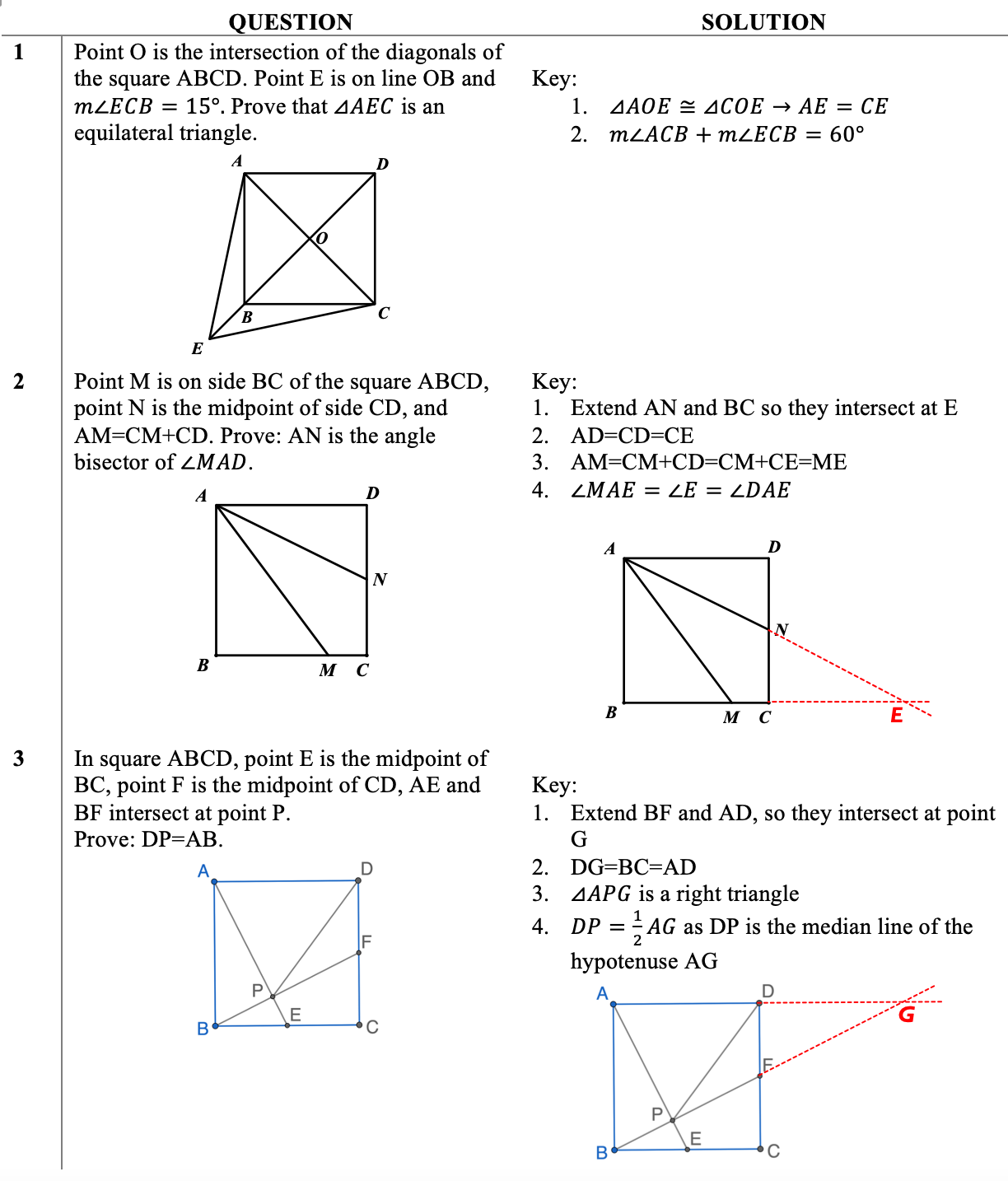
After a month of study, it becomes evident that all students, irrespective of whether they commenced with a head start or not, converge at the same juncture upon mastery of the essential theorems, poised to embark upon the subsequent phase of geometric proof. Question 2 serves as an introduction to the application of “auxiliary lines” in solving intricate geometric problems. In the beginning, it is challenging for almost all the students in my class, even though these students are in honor level. The learning process predominantly unfolds through two paths: rote memorization and deductive reasoning. Jerry is a representative of the students who embrace geometric proof mainly by rote memorization rather than deductive reasoning. I’m really touched by his effort that he notes down every detailed step written on the whiteboard and each seemingly pivotal strategy imparted during lectures. After class, he also works on extra exercises in addition to homework in order to reinforce his memorization and comprehension. If he sees “midpoint” in a similar question, without further contemplation, he will extend the line segment bisecting the midpoint to construct congruent triangles, just because that’s what the class example said. If he gets stuck with a new problem such as Question 3 in Table 1, he knows that he may add the auxiliary line(s) in the wrong way or he just can’t move further with the correct auxiliary lines, but he feels frustrated to find another way to solve the problem. In essence, he also uses deductive reasoning upon mere memorization, but his deductive reasoning ability is limited to low-cognitive problems. While rote memorization yields some efficacy, it does not help much with solving novel and challenging problems.

High-Cognitive
Students prefer deductive reasoning also memorize the key hints: midpoint implies extending the line segment to creative congruent triangles. Other than memorization, they also try backward and forward logical reasoning — bridge the gap between the given premises and the statement through trial-and-error. In Question 2, 
1. What does the equality AM=CM+CD imply? 
2. How can the algebraic expression be translated into geometric relations?
3. How important is the midpoint N and square in relating the given information and the unknown? 
4. Angle bisector implies two congruent angles; The measurements of the angles are not given, so to prove two angles are equal, students can use either congruent triangles or isosceles triangle. Which is more feasible?

To answer the first two questions, students notice the requisite alignment of line segments CM and CD. The alignment can then be used to compare the combined length of line segments CM and CD with that of AM, which provide clues for the introduction of auxiliary lines. By extending MC and AN, two congruent triangles ADN and ECN are constructed, which subsequently paves the road to reach the final statement.

Question 3 is given to the 8th graders after right triangle and the properties of median lines are introduced. While akin to Question 2 in its utilization of squares and midpoints, Question 3 covers more theorems and needs more steps to unlock.
1. If DP is equal to AB, then DP is equal to any side of the square. Which side can simplify the problem?
2. DP and AP are in the same triangle ADP, but it is hard to prove that angle DAP is equal to angle DPA (It’s an alternative way but students haven’t learned trigonometry yet). 
3. There are two midpoints E and F. If auxiliary lines are based on midpoints like Question 2, which midpoint is better?
4. Extending BF and AD creates two congruent triangles BCF and GDF and corresponding sides BC and DG. Prove DP=DG?
5. It’s hard to prove DP=DG. Does it mean the auxiliary lines are not useful?
6. Are all the given information used? What does midpoint E indicate? 
7. Is point P special? It is the intersection point of AE and BF. What does this tell?
8. AE is perpendicular to BF and point P is the foot, therefore, triangle APG is a right triangle. 

The breakthrough lies in the median of the hypotenuse of the right triangle APG. In my annual honor-level math class, no more than three students are able to independently solve Question 3 successfully each year. Among all these students, some of them not only possess a head start but are consistent top performers; there also exist students who, despite not initiating with a head start, promptly assimilate novel concepts and showcase a profound grasp of underlying principles. Other students, including those learn in ahead, either construct the auxiliary lines in the wrong way or encounter obstacles when proving DP=DG. Upon knowing all the relevant knowledge, students also need to make efficient interrelations between the premises and the theorems, which is the essence of deductive reasoning, the most challenging part of geometric proof. Thus far, the advantages conferred by a “head start” have been expended. What then distinguishes students from one another is their ability in deductive reasoning.

A Head Start in Deductive Reasoning?
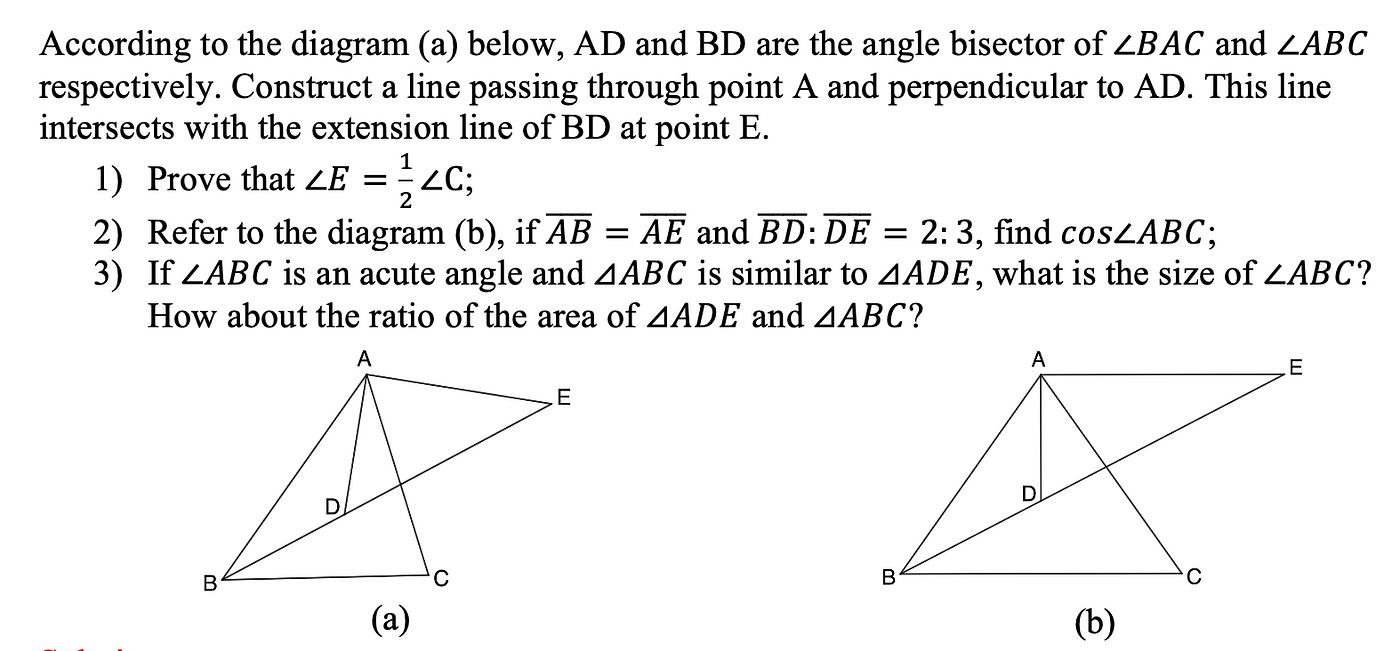
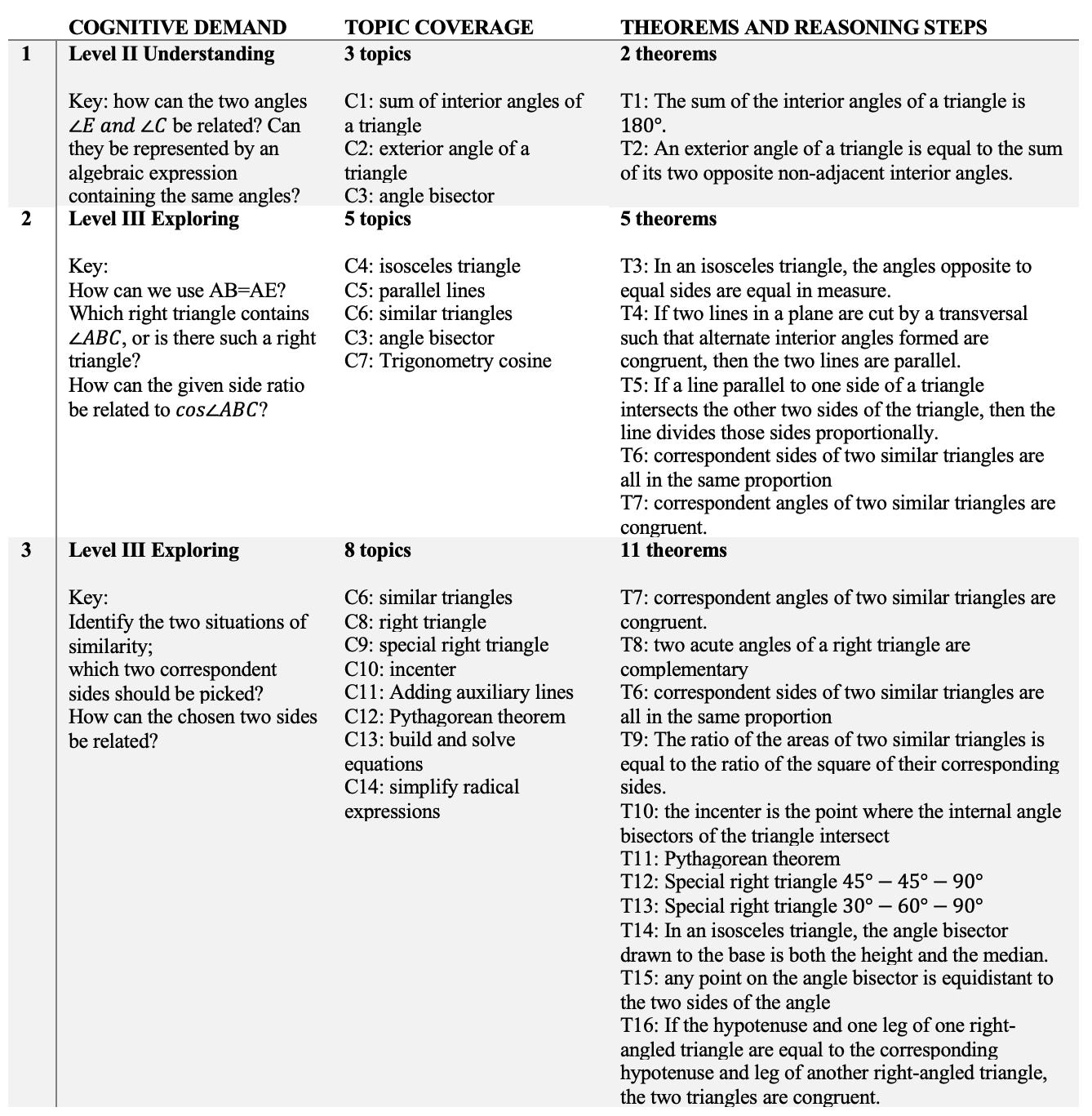
Then why not provide students with a head start in deductive reasoning? Indeed, students engage in early learning during the summer or the winter breaks also learn reasoning skills, but this reasoning is relatively at a low-cognitive level. However, in the selective exam-oriented educational system in China (take Shanghai as an example), geometry, especially geometric proof, serves as a tool to discern students’ academic potential. Geometry accounts for over 40% in the Shanghai High School Entrance Examination each year (Shanghai Zhongkao Mathematics). The last question, the one that distinguishes students, remains to be the most challenging comprehensive geometric proof inquiry. Take the 2019 Shanghai Zhongkao Mathematics as an example, Question 25 (Figure 1) is composed of three sub-questions. According to the cognitive demand framework outlined in the 2019 Shanghai Middle School Mathematics Curriculum Final Guide, the first sub-question is at level II understanding, while the other two are both at level III exploration. The last sub-question covers eight topics spanning from algebra to geometry and necessitates the employment of 11 theorems throughout the course of its proof (as detailed Table 2). Evidently, this question is more cognitively demanding than Question 3 in Table 1. Honestly, the journey from questions in Table 1 to the last question in the high school entrance examination is an arduous endeavor spanning about three years filled with repetitive practice. However, even with the same amount of practice, fewer than 10% of the students (out of about 50,000 students took the exam in 2019) successfully solved the last question. So, does a head start in deductive reasoning offer a significant advantage? Regrettably, a head start doesn’t make any difference in solving the high-cognitive challenging problems.

Ironically, it’s noteworthy that not every secondary school mathematics teacher can tackle the final question, despite their wealth of accumulated experience and prior knowledge. This situation is akin to my own inability to solve the geometry questions presented in the International Mathematics Olympiad. Does it mean that deductive reasoning is exclusively an innate ability, and we should give up if we were not born into a geometry person?

Teaching Strategies and Heuristics to Improve Reasoning Abilities on Individual Basis
Drawing from my experience teaching secondary school students and my personal learning experience, I contend that while innate ability may indeed play a role, the transformative impact of appropriate instruction and effective practice should not be underestimated. Those who possess stronger reasoning abilities than their peer groups also improve through practice. They seem to have intuitions when making decisions during problem solving, but this intuition does not come naturally, rather, it comes from experience and prior knowledge (Schoenfeld, 1982). Therefore, our emphasis should center on enhancing individual deductive reasoning skills rather than engaging in comparative evaluations with others. In sum, deductive reasoning skills are teachable, although the extent to which they can be effectively imparted on an individual basis may vary. Educators should actively employ strategies and heuristics aimed at nurturing and cultivating students’ capacities for sound reasoning.

References

Schoenfeld, A. H. (1982). Some thoughts on problem-solving research and mathematics education. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 27–37). Philadelphia: Franklin Institute Press.

2019 Shanghai Middle School Mathematics Curriculum Final Guide.