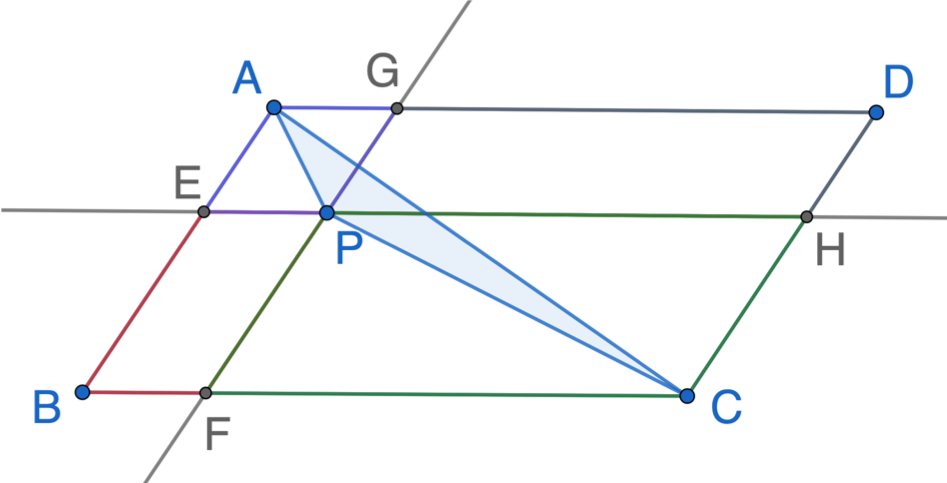
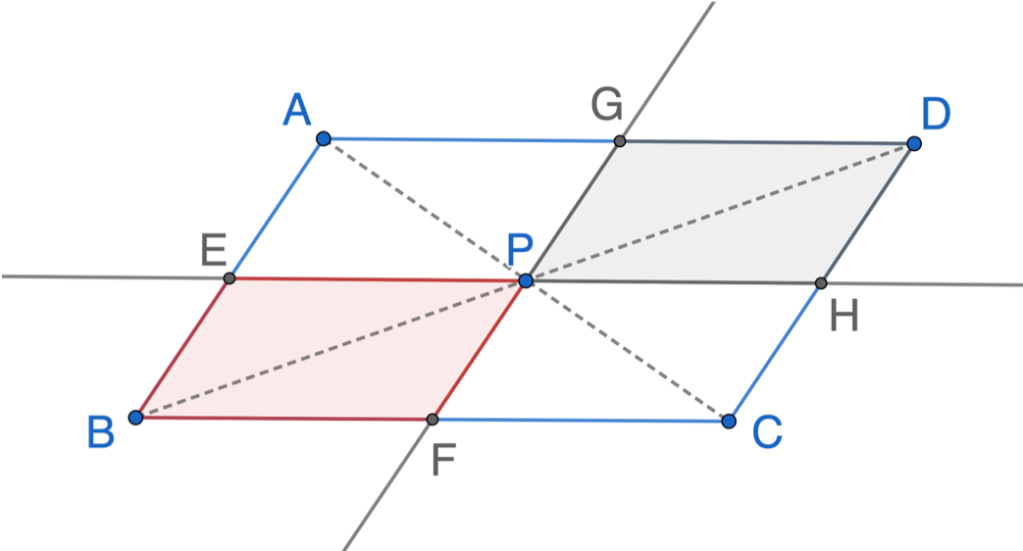
Given that P is a point in parallelogram ABCD, line GF passes through point P and is parallel to AB, line EH passes through point P and is parallel to AD. If the area of BFPE =3,the area of PHDG = 5, find the area of ▵APC.
Area of a triangle?
- Formula: Area=1/2 base∙height
It is quite hard to get the length of the three bases. It is even more difficult to get the height on each base. Therefore, this method doesn’t work. - Cut the triangle into parts Cut the triangle into 2 or 3 smaller triangles makes the situation even more complicated.
- Subract from a bigger shape The area of ▵APC can be subtracted from quadrilateral APCD and ▵ABC. We need to explore now!
Method 1: Use Triangle ABC as a whole
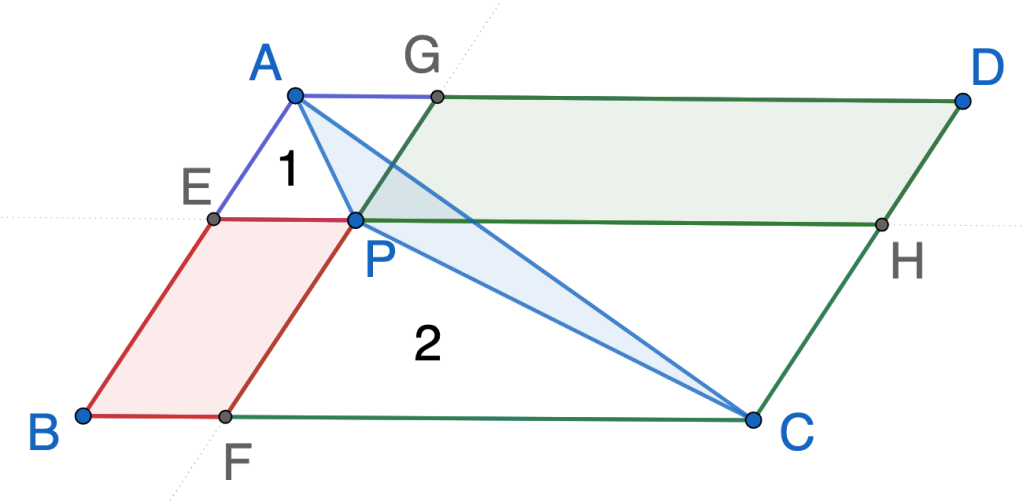
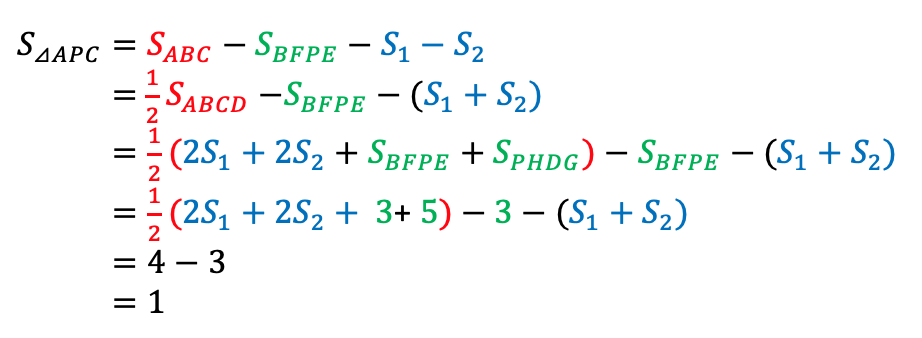
Method 2: use Quadrilateral APCD as a whole
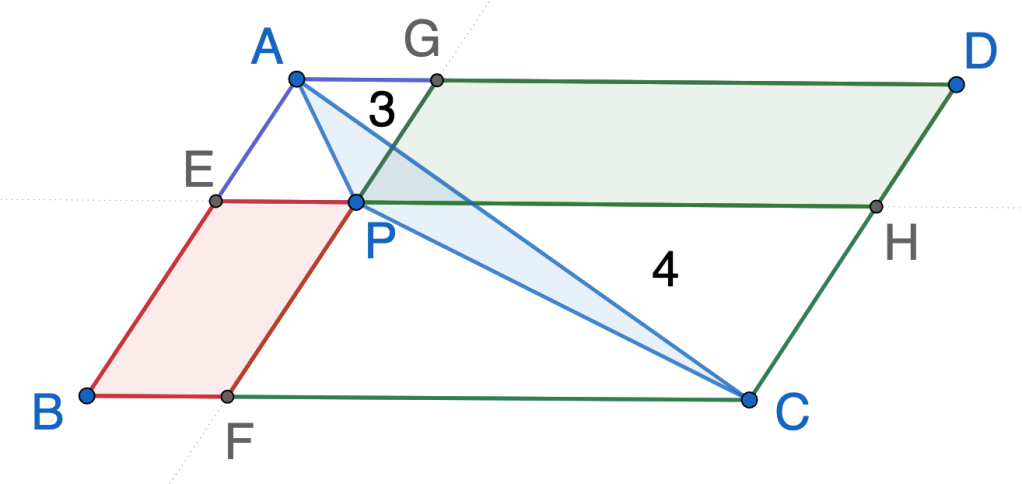
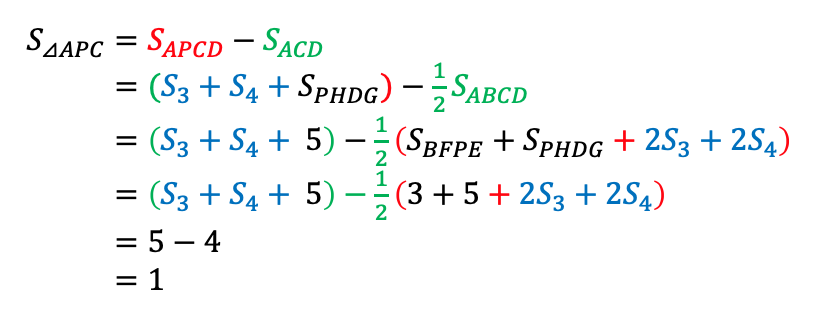
Key Points
- The diagonals of a parallelogram cut the parallelogram into two congruent triangles.
- Point P is not a special point, it can be anywhere inside of the parallelogram. As long as there is a triangle APC, the location of P is not important.
- The magic part of subtraction is that you can subtract those unkown parts or variables in Algebra. So don’t be afraid of those unkowns.
Geometry is art!
A visual representation will open a new door for you.
Leave a Reply