My son could say numbers from 1 to 10 in both Chinese and English at age 3. However, numbers to him were nearly the same as Peppa Pig to him, which were merely words with distinct pronunciation. He couldn’t count the number of toy cars he owned due to a lack of sense on numbers or the numerical orders. This raised a question: if kids are not taught numbers, can they obtain the numerical skills by themselves one day?
I didn’t realize how unrealistic I was until I read the book The Story of Mathematics. The number system we take for granted today is built upon thousands of years of accumulation of human wisdom. The role of Mathematics, in particular, is always the catalyst of human civilization.
Take counting numbers as an example, there is a story. Once upon a time, there was a small kingdom in the foothills of the Youshan Mountains in China, and the prince of the kingdom was a young man surnamed Chen. One day, the prince caught a tortoise by the sea, and when he returned to the village, he said to the soldiers: “I caught a lot of tortoises today.” At that time, he proudly lifted the lid, but there were only 3 turtles in the cage. The soldiers still cheered: “Wow! There are so many turtles!” As people in this kingdom had no idea about numbers such as 3 and 4, they only divided all numbers into 3 categories. Except for 1 and 2, the others were “many”.
Even with the decimal system commonly used in the modern world, Babylon once described the numbers like this:

It is inconceivable that by how long a series of patterns must be drawn in this way to exactly describe the housing price of tens of millions of dollars nowadays in Shanghai. Even though the Arabic numerals are dominant in the world, the west and the east use quite different place values:
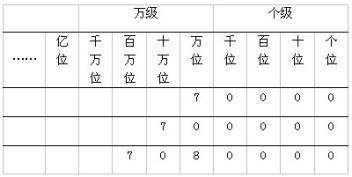

Obviously, even the most basic part of mathematics implies the powerful logical ability. Different from visual stimulation, mathematical abilities refresh human cognition through deeper thinking and reasoning. And this kind of ability, begins to show up and permeate in middle school in Shanghai, is precisly the essential difference between elementary school mathematics and middle school mathematics.
From Arithmetic to Mathematical thinking
Some students struggle with the transition from calculation to deep thinking in middle school mathematics. There are three main reasons:
- Lack a solid arithmetic foundation in elementary school
In elementary school, few mathematical theorems are involved in raising the level of human cognition, instead, “numbers” and “calculation” are the main abilities which can be improved through repeated mechanical training. However, in the context of Chinese exam-oriented education, if a student fails to build reflexive computing skills in elementary school, he or she will be unlikely to follow up with more complicated calculation in middle school. As a result, such students are still making up for calculation when the talented students have upgraded to analysis, reasoning, and speculation.
2. Taking notes without thinking
These students have developed a “good” study habit in elementary school. They immerse themselves in taking notes and memorizing the steps of each question word by word in class. Their notes can always attract many other students to borrow, especially when a final exam is to come. In sharp contrast to their detailed notes, their grades were just mediocre. In middle school, this “good” study habit needs to extend from “mechanical repetition” to “analytical thinking”. Yes, it is the ability to think deeply, critically and thoroughly that distinguishes students as the grades go up. Truly, students have to step out of their comfort zone to go across the leap in advanced thinking.
3. NOT strive for perfection
Understanding all the concepts and theorems may be enough to achieve an outstanding score on SAT but far from adequate to succeed in the national exams in China. Some students possess strong comprehension ability and enable to put forward new ideas sometimes but their test scores are just at the average level. It is not the so called IQ that separates them from top students, rather, it is the attitude to detail every single step that widens the gap between average students and top ones. Why is that? Chinese math tests, unlike most western countries where multiple choice questions are prevalent, emphasize on detailed steps (format), geometry proof in particular, prioritizing students’ thinking process over final results. Without deliberate practicing through daily homework, it is impossible to meet the requirements of the tests. To put it another way, the quality of perseverance and the extent of details eventually form ever-increasing disparities among people.
Mathematical Thinking plays a key role in Chinese math education
Malcolm Gladwell, the author of Outlier, put forward the 10,000-hour theory, revealing the accumulation of knowledge behind Bill Gates’ success. The inspirational film The King’s Speech also reveals that consistent deliberate practice is the key to success. In fact, the 10,000-hour theory is a perfect demonstration of the traditional Chinese testing. However, even though students spent the same amount of time and solved the same number of questions, their way of learning associated with efficiency eventually lead to radically different test results and overall ability. Some parents think it wrongly that the reason of children scoring higher is because they have practiced a lot more. Actually, it is the way of learning efficiently and effectively that leads to the gap among students in terms of knowledge and wisdom.
Let’s first look at the skills and abilities required by the Shanghai High School Entrance Examination (2018 Zhongkao):
Basic knowledge and basic skills 49.3%
Logical reasoning 14.7%
Calculation 10.0%
Space concept 11.3%
Problem solving ability 14.7%
Most students were in the 136-140 score segment. That is to say, in the high school entrance examination with nearly 50% basic knowledge and basic skills, it is not difficult for students to get 136 points in the test as long as they study hard. As a selective exam, what distinguishes students are these abilities: logical reasoning, spatial concepts, and problem-solving skills. Students got 140-145 have a good mastery of the above but may fail in one or two extremely hard questions whereas those above 145 to 150 not only have a “math brain” but also “extraordinary qualities”.
4 Stages of learning math
The duration of math education for a typical university graduate majored in science or engineering in China is 16 years, beginning with 6 years in elementary school, 3 years in middle school followed by another 3 years in high school and finally 4 years in university. To get a Bachelor’s degree in science or enginering, one has to firstly outperform peer groups in the high school entrance exam and then the national college entrance exam 3 years later. On top of that, mathematics is generally considered the subject that tells students apart from different tiers of universities.
Based on my own learning experience as a reference, I would like to divide the learning process into four stages:
- Asking questions: Knowing why?
Linear algebra is a compulsory course in university, the most difficult one for me. On the one hand, the transformation of matrix follows no formula. On the other hand, I don’t understand the meaning of this transformation. Many years after graduation I saw the picture shown on Matrix67’s blog – the “linear pull” of the plane is transformed through matrix multiplication, I instantly hit the essence of linear algebra. Moreover, I suddenly understand what a Fourier transform means.

In fact, many students often question why they have to learn mathematics? With students’ limited knowledge and experience, it is difficult to understand the knowledge framework, knowledge progression and knowledge extension. Questioning is valuable. When we question, we might as well explore the history of mathematics. Why did the ancestors do this and what is the story behind it? Is there a better way to deal with it? Perhaps, these amazing discoveries will arouse our interest and broaden our knowledge.
2. Training: quantity changes lead to quality changes
Some researchers doubt the importance of homework. Homework, classwork, quizzes, or any other forms of training, are absolutely necessary in math education. Is understanding of the concepts enough? Knowing the theorems to prove congruent triangles only helps students solve straightforward one step geometry proof questions as these questions don’t involve any deep logical thinking. However, a typical congruent triangle question in China is like this:

Is this question asking to prove congruent triangles? Why congruent triangles are needed to relate the three line segments? Exactly, all the conditions are given in a hidden way. Without training, most students even don’t know what the question is asking for? Honestly, this question is merely medium level in Chinese math. Only through repeated training can a student quickly get the key clue and therefore finish a test in limited amount of time.
3. Summarize: from memorization to understanding
After a certain amount of practices, we can calculate the GCF greatest common factor and LCM least common multiple by “short division” quickly and accurately. Let’s take a look at the two word problems.
Alice works for a florist shop. She has 96 lilies and 72 white roses. She wants to put all the flowers into bouquets with each bouquet having the same number of flowers in it. Without leftovers, what is the greatest number of flower bouquets? GCF(96, 72)=24
Brian has swimming lessons every fifth day and dancing lessons every third day. If he had a swimming lesson and a dancing lesson on July 5, when will be the next date on which he has both swimming and dancing lessons? LCM (5, 3) =15
If students are trained to solve the two word problems by those so called exam skills – find GCF when the word greatest is in the problem, similarly, find LCM if the word least is there, students would not explore the essence themselves.
- Distribute a set of data – find the common factor
- Integrate a set of data – find the common multiple
Only when we truly understand mathematical knowledge and make our own generalizations can we turn knowledge into wisdom.
4. Comprehensive Application: Extracting Information-Integrating Information

This is the last question of the 2019 middle school math proficiency test in Shanghai (Zhongkao). The three questions cover many contents, such as angle bisector, special trigonometric ratio, similar triangle and triangle incenter. Question 3) is challengeable in two ways. Firstly, there should be two cases according to the given information. Secondly, none of the side length is given but is needed to get the area ratio of the two similar triangles. The key to find the side ratio lies in the special right triangle and
. Besides, the property of the incenter is the adhesive of the sides in two similar triangles.
What information is given?
What is unknown?
Can the unknown information be derived from the given ones?
If not, are auxiliary conditions available?
If not, can the problem be transformed into an accessible one?
Though hard, it is just a question on the test. The real world is more complicated than a test. Therefore, the skills of extracting information and integrating the known to infer the unknown will be pivotal in adulthood. Furthermore, interdisciplinary knowledge is inextricably tied together to tackle the real cases in the evolving world. This is a process that involves modern heuristics, which not only tests the mathematical thinking ability, but also requires a person’s perseverance.
There is no shortcut! Deliberate training is essential to transform knowledge into “wisdom.”
At a young age, it’s hard for us to understand the need to learn those abstract knowledge. But when we forget what we have learned, The rest is the “wisdom” that we have obtained along the way.
Leave a Reply