“Mommy, do you know how many bars of chocolate are there?”, Shawn asked when he opened the pack of chocolate.
“Hmm, there are 24 bars”, I replied in about 2 seconds.
Shawn, “how can you count the total numbers so quickly? I didn’t count but tried to add 6 bars four times, yet I’m still slow, much slower than you”. 
Me, “Honey, I used 6*4=24. This is multiplication, which is more efficient than adding the same number repeatedly.”

Since then, Shawn understands the meaning of multiplication 6+6+6+6=6*4=24
When it comes to multiplication, I naturally think of multiplication tables and rely on the method of ‘long multiplication’. However, he does multiplication by drawing and adding all the time.

If Shawn is asked what is the product of 7 and 13, he would draw 13 sticks in a line and repeat 7 times (Figure 1). Later on, he noticed some kind of shortcuts to do the repeated addition quickly. Instead of adding 13 seven times, he first added 13 to 13 and get 26, then 26+26+26=78, so far, he added 13 six times, and finally added the last 13 to 52 to obtain 91. Although still slow, he actually used “distributive property”, this cognition through geometric illustration surprised me and ignited my thinking of teaching kids long multiplication through the distributive property. If I’m asked what is 17 times 3, I would just follow the multiplication formula, mentally. And now I realized how abrupt to introduce the formula to a novice and how important teachers understand and respect kids’ cognition process.

It was such a coincidence that I was taking the course named “Mathematics for Machine Learning: Multivariate Calculus” offered by Imperial College London on Coursera. The professor visualized the product rule using the area model and it is intrinsically the same as distributive property in elementary school. Ironically, it is the first time that I get to understand ‘Calculus’ after finishing my undergrad and graduate study for over 10 years. Calculus to me used to be barely formulas and hundreds of algebraic manipulations upon the formulas, e.g., chain rules (product rule). Given f(x)=xsinx, I can find the derivative using the formula easily, even without thinking:
f’(x)=(xsinx)’=x’sinx+xsin(x)’=sinx+xcosx.
As a student, I didn’t ever think about the logic behind all the formulas, in another way, formulas are enough to solve calculus problems, so why is logic important? One can solve difficult differential equations with strong algebraic skills but can’t apply them well without knowing the underlying logic. Identically, the basic logic under machine learning is the foundation for further exploration and advancement. Teaching strategies in advanced math can also affect undergraduate learning. Geometric illustration of an algebraic problem is essential to enforce students’ understanding. Technology also provides more possibilities for educators to tailor the appropriate demonstration to students.

From elementary to advanced mathematics, the same geometric illustration, as well as the same thinking method, is used. Looking back, the connection between knowledge and the human cognition process may provide new insights for K-12 mathematics education.

Area Model in Elementary School Math-Numbers

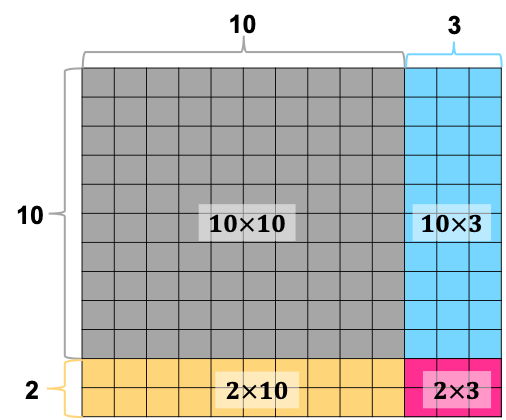
As Figure 2 shows, it’s natural to make 13 columns into 10 and 3 columns not only because any natural number multiplied by 10 is easy to get but also because we use the base 10 system. The grey part holds 10 columns and 7 rows of squares, 7*10=70; the blue part is composed of 3 columns and 7 rows of squares, 7*3=21. The total number of squares is the sum of 70 and 21, which gives 91. The distributive property involved here can be written:
7*13
=7*(10+3)
=7*10+7*3
=70+21
=91

This perfectly explains the long multiplication method below. Instead of using the traditional way of expression called regrouping tens, it makes more sense to write it following the distributive property to a new learner, especially when larger numbers are introduced.

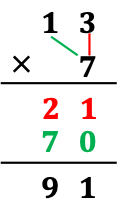
Take 13*12 as an example. 13=10+3 and 12=10+2. The geometric illustration (Figure 3) shows that the 13*12 squares can be distributed into four parts: the grey part with 10 columns and 10 rows, the yellow part with 10 columns and 2 rows, the blue part with 3 columns and 10 rows, and the pink part with 3 columns and 2 rows. The whole calculation process can be written:
13*12
=(10+3)*(10+2)
=10*10+10*2+3*10+3*2
=100+20+30+6
=156

It is exactly how long multiplication works.

Area Model in Secondary School Math-Variables

Many students have struggled with the transition from numbers to variables. This probably is the first transition from elementary to secondary school math worldwide. Many students feel it is hard to step over. Researches reveal that the leap can be smooth with a continuous and connected curriculum (H.Wu, 2001). Chinese students have a strong arithmetic background and start to learn to solve simple linear equations in Grade 5/6 but still suffered more or less. Curriculum design is one aspect, but knowledge presentation is somewhat more realistic in teaching. Geometric illustration undoubtedly helps ease the leap from concrete to abstract. For example, the multiplication of polynomials and hence factoring polynomials can be well demonstrated by the combination of rectangles. As an adult, we intuitively choose the FOIL method to multiply polynomials, e.g.,(x+1)(x+3)=x²+3x+x+3=x²+4x+3
which is a conditional reflex after repeated practice. FOIL is introduced in some classes directly and surely students can master the steps whatever, however, many students just automatically remember the steps without understanding, only some may discover that it is actually the same as the way distributive property is used to calculate 13*12. Adding the areas of the four parts x², 3x, x, and 3, the total area, the value of (x+1)(x+3) is obtained (Figure 4).

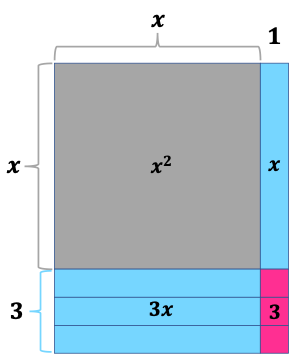
What’s the difference then? For multiplication, there’s no big difference whether you understand it or not, but for factoring and solving quadratic equations, it matters a lot. Factoring a quadratic trinomial is to write it in the form of a product of two linear expressions. x²+4x+3 is a quadratic trinomial factorable in integers, meaning that algebraically we can easily use cross multiplication to factor it. What is the basis for cross multiplication? Generally,
x²+bx+c=(x+x1)(x+x2) where x1+x2=b and x1*x2=c. 
If a quadratic trinomial is the area of a rectangle, then Factoring is expressed in width times length. Geometrically, the blocks or tiles have to be arranged appropriately to fit the area. Figure 4 is a perfect fit. In contrast, with a corner missing, Figure 5 is not even a rectangle, though the total area is also x²+4x+3. Now, it is clear how cross multiplication works, we first need to find two numbers whose product is c, in the meantime, the sum of the two numbers must be b, in order to form a rectangle given the area.

Graphically, factoring means that given the area of a rectangle, find the dimension. To factor x²+4x+3, first focus on 3, which can only be written in the product of 1 and 3, second, the sum of 1 and 3 is 4. Algebraically, we also solved
x²+4x+3=x²+x+3x+1*3=x(x+1)+3(x+1)=(x+1)(x+3)

Turn to Figure 5 again, although the tiles can’t add up to x²+4x+3, it reveals that a perfect square (x+2)² is formed by adding 1 to x²+4x+3. This explains the method of completing the square.

In addition to factoring quadratic trinomials, the area model also helps understand solving quadratic equations geometrically. Given x²+4x+3, the area of the rectangle in Figure 4 is 0, either width or length is or both of them are 0. When the width is 0, x+1=0, x=-1; when the length is 0, x+3=0, x=-3. Therefore, the solution to the quadratic equation is
x=-1 or x=-3

Area Model in Advanced Math-Calculus

As I mentioned in the beginning, the graphical demonstration of the product rule enlightens and refreshes my understanding of formulas. Given h(x)=f(x)g(x), you may know the derivative of h(x) is
h’(x)=(f(x)g(x))’=f’(x)g(x)+f(x)g’(x)
Do you also know why?

When delta x (dx) is near 0, f(x+dx) is nearly the same as f(x) and g(x+dx) is also extremely close to 0. Therefore, [f(x+dx)-f(x)][g(x+dx)-g(x)] is near 0, meaning the area of the pink rectangle can be neglected compared with the blue and yellow area. The expression can then be written as follows:

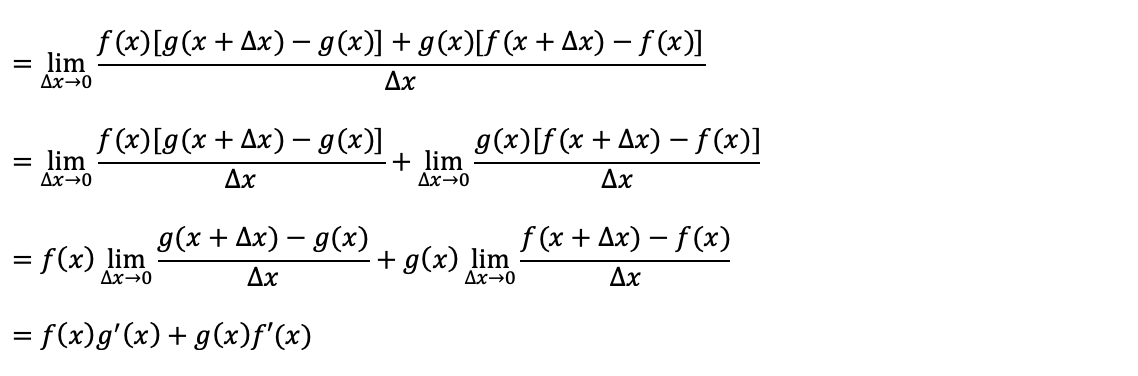
Now, it’s clear why h’(x)=(f(x)g(x))’=f’(x)g(x)+f(x)g’(x).

Conclusion

1. From elementary to secondary school to advanced mathematics, area models are used for numbers, variables, and functions, following the same theory. It may not be necessary for an elementary school math teacher to know advanced math, but it certainly helps if teachers know the thinking methods involved in both k-12 and advanced mathematics. In addition to curriculum design, teacher education associated with teaching strategies are more important in smoothing the transition from elementary to secondary school math and from high school to advanced mathematics.
2. Introducing a new concept to a beginner is the art of teaching strategies, whether the learner is a child or an undergraduate. Geometrical illustration can greatly enhance students’ learning as those abstract concepts and formulas are better explained graphically than verbally.

Reference
H. Wu, How to prepare students for algebra, American Educator, Summer 2001, Vol. 25, №2, pp. 10–17. http://www.aft.org/pubs- reports/american educator/summer2001/index.html