To figure out why Chinese students top in PISA and other math competitions, let us turn to ‘Zhongkao’, which appears to be completely different from PISA but reveals how the math abilities required in PISA are obtained through math education. PISA’s targeted students are those 15-year-olds and meanwhile enrolled at grade 7 or higher. In the B-S-J-Z population, students at 9th grade and 10th grade count for 96.9%[1]. In the Chinese education system, 9th grade is the last year of middle school and 10th grade is the first year of high school. From middle school to high school, students need to climb the first mountain in their lifetime – Middle School Academic Proficiency Tests, locally known as ‘Zhongkao’, given once a year in the mid-June for all the registered students in Grade 9 (around 15 years old). In Shanghai, subjects such as Chinese, Mathematics, English, Physics and Chemistry, and Sports, are tested and counted toward the overall score. More subjects are added including History, Civics and Law, and Interdisciplinary Case Analysis, thus more abilities and skills are required since 2021. On one hand, this is a national graduation exam after 9-year compulsory education. On the other hand, it is also the High School Entrance Examination due to its selective essence. In reality, students are ranked according to the overall test scores of all the subjects and matched with high schools from top 1 to the last. Among all the subjects, Mathematics is widely recognized as the most challengeable one. Shanghai has attended PISA each year ever since 2009, a close look at Shanghai Middle School Mathematics Proficiency Test will walk us into math education in Shanghai, China.
Structure, Format and Contents of Test
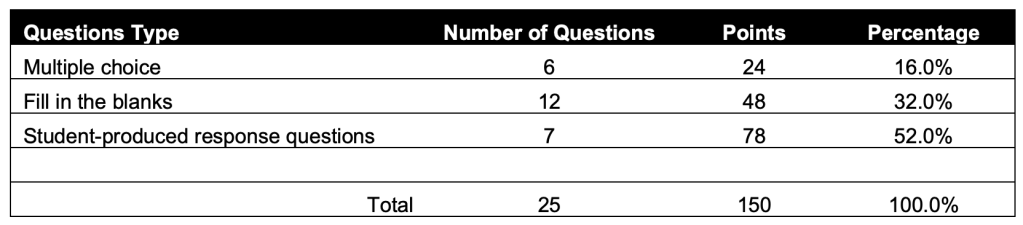
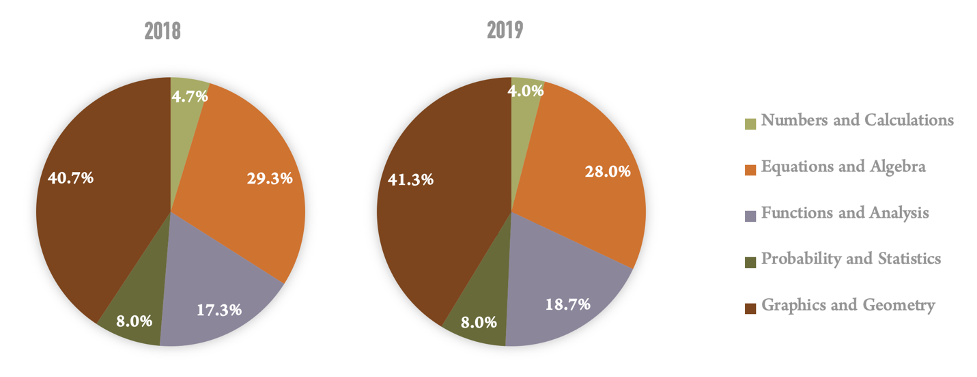
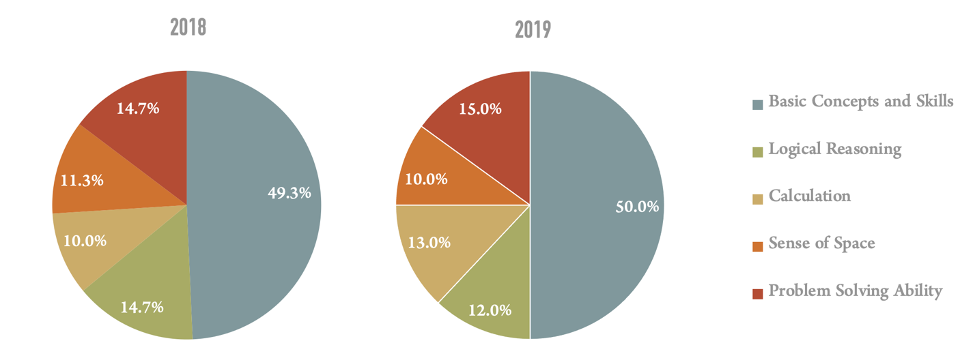
The exam structure is exactly the same each year, composed of three parts: multiple choice, fill in the blanks and student-produced response questions. Students are given 100min to finish 25 questions, with some of them containing two or three sub-questions. Refer to Table 1 for detailed composition of the question types and the associated scores. The contents covered throughout middle school math includes five aspects (Figure 1) with a focus on geometry, equations and functions. Five types of mathematical abilities are tested (Figure 2): understanding basic math concepts, doing some complex calculation without a calculator, having the sense of space, able to think and reason logically, and applying the knowledge to solve real world problems. Middle school graduates with 9 years’ compulsory education in Shanghai are supposed to have acquired these five abilities. Among the three question types, student-produced response questions account for the highest proportion, mainly composed of mixed calculation, solving equations, the application of functions in word problems, quadratic function and analysis, triangle or quadrilateral proof, and geometric questions combined with circles and triangles, covering the main contents taught in middle school. Therefore, this section will thoroughly demonstrate student-produced response questions selected from the former proficiency tests in order that readers get to know the details and requirements of math teaching in Shanghai.
Some questions selected from the past tests


[Comment]
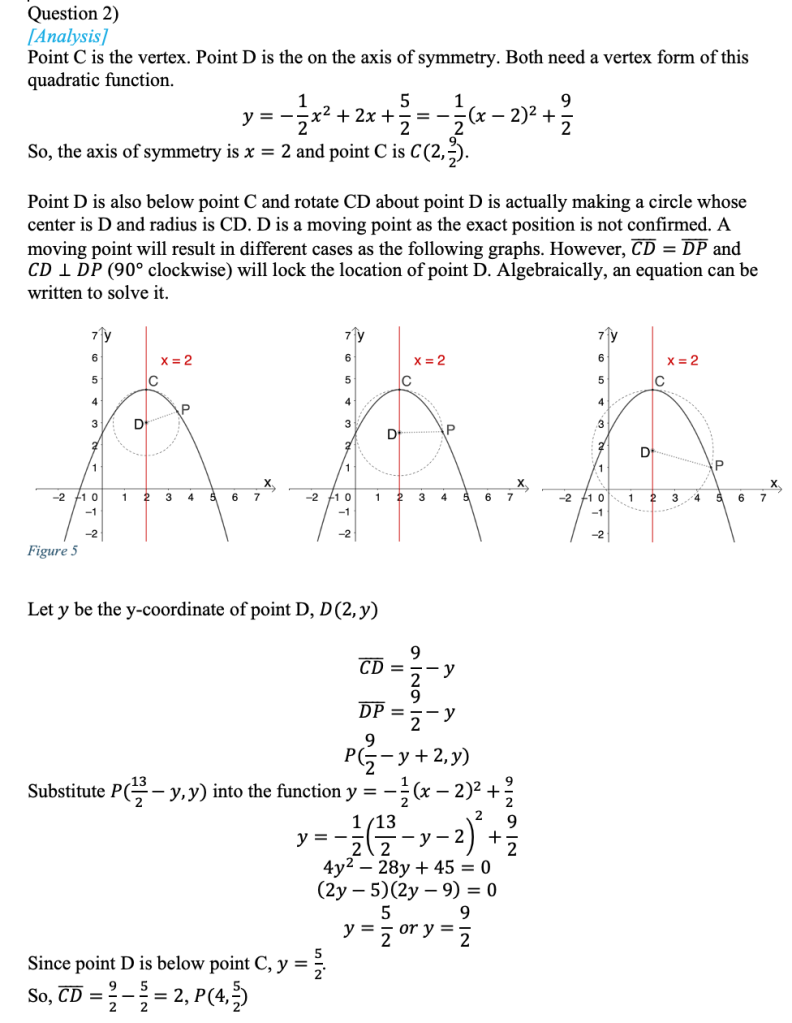
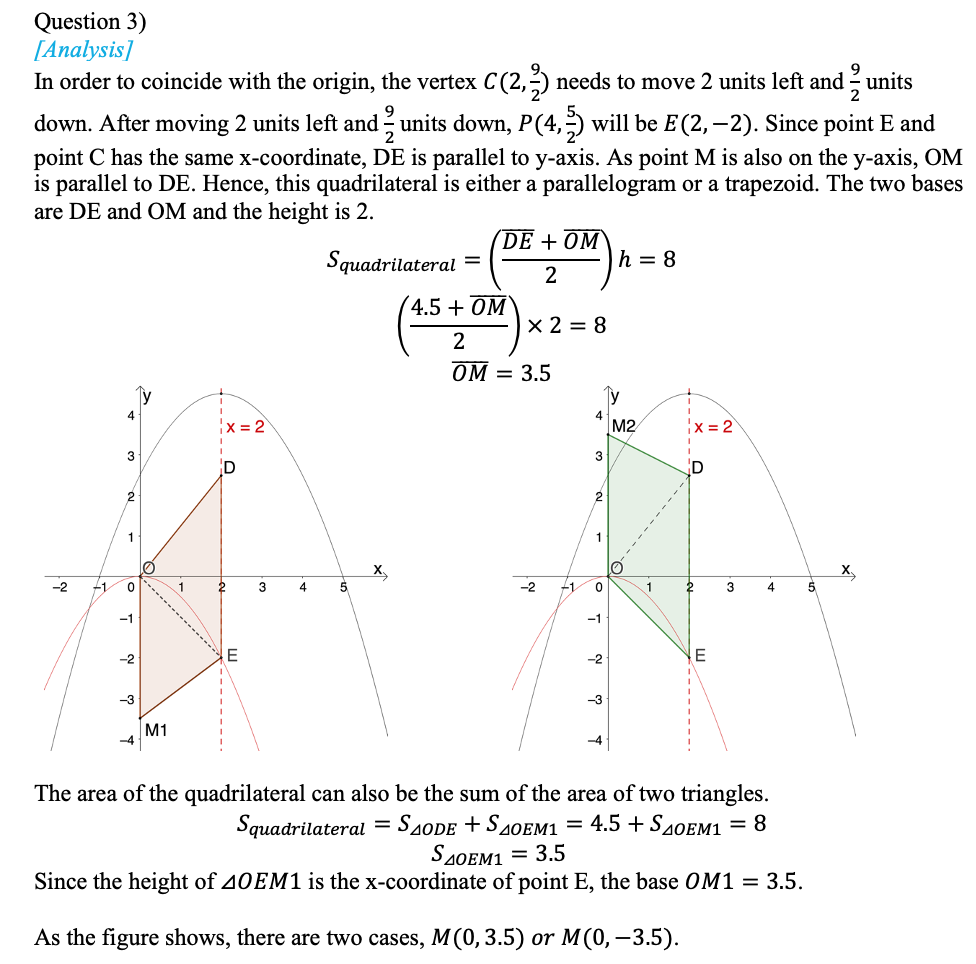
The first question is straightforward with a difficulty factor of 0.85. Students can substitute the given points to the function to get the analytical expression. The second question (difficulty factor 0.70) requires students to have a sense of space, imagine a moving point and relate graphics to the quadratic function. The last question (difficulty factor 0.40) is about translation of the parabola. Students need to find out the corresponding points to sketch out the shape of the quadrilateral. Finally, students are supposed to be rigorous enough to include both cases.
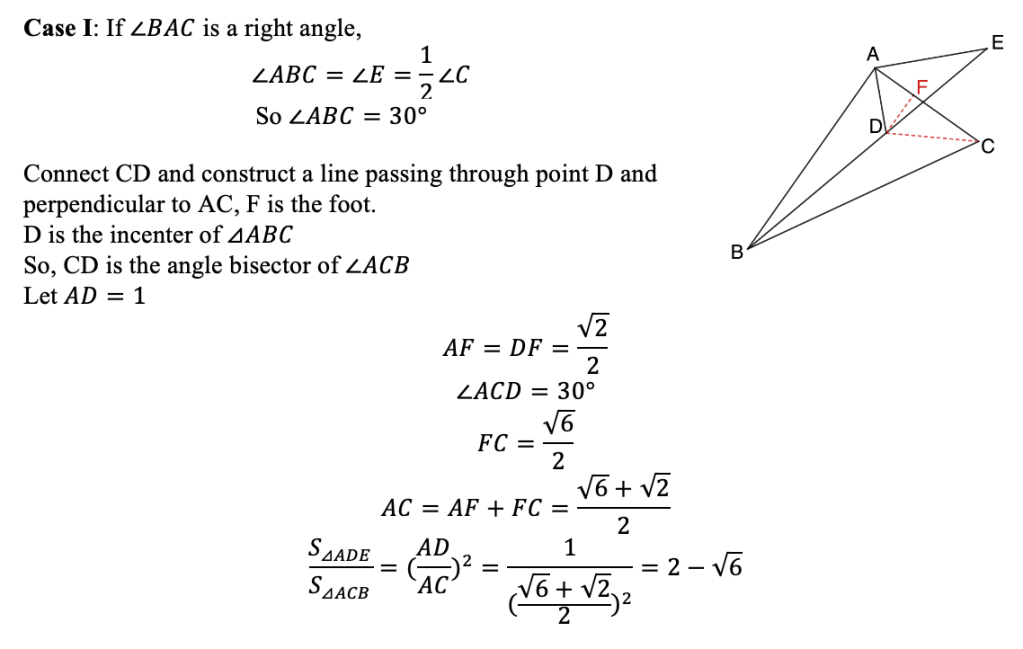

[Comment]
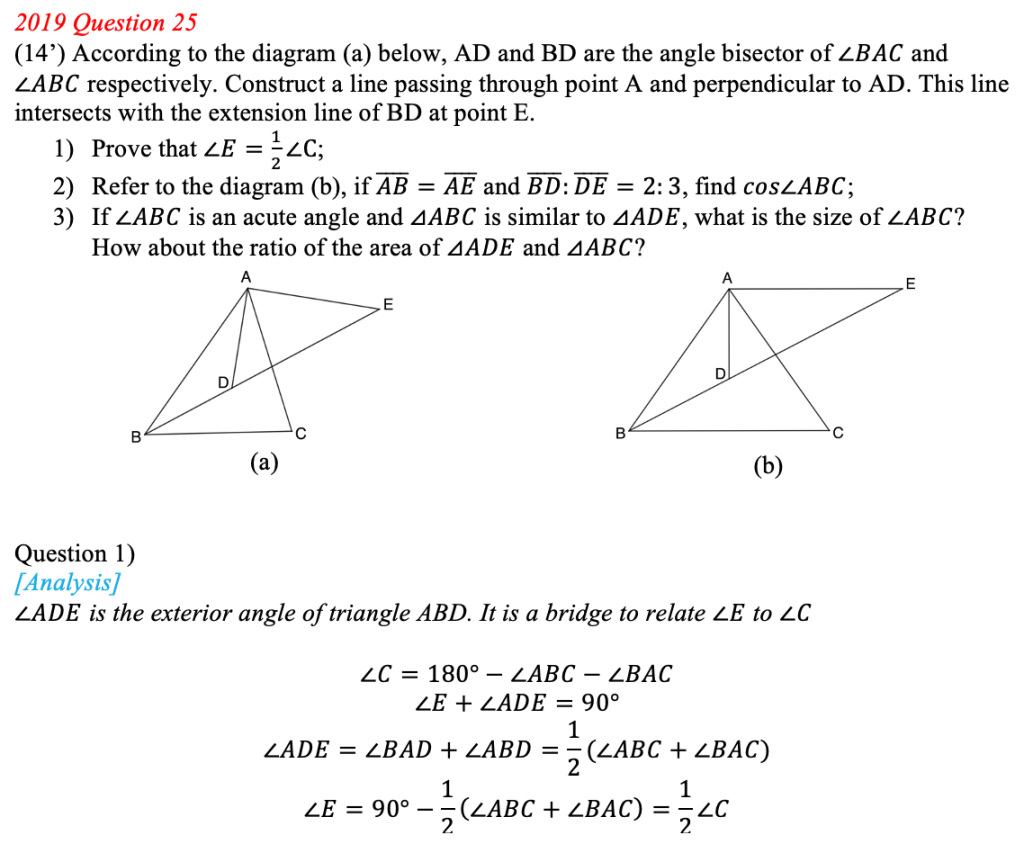
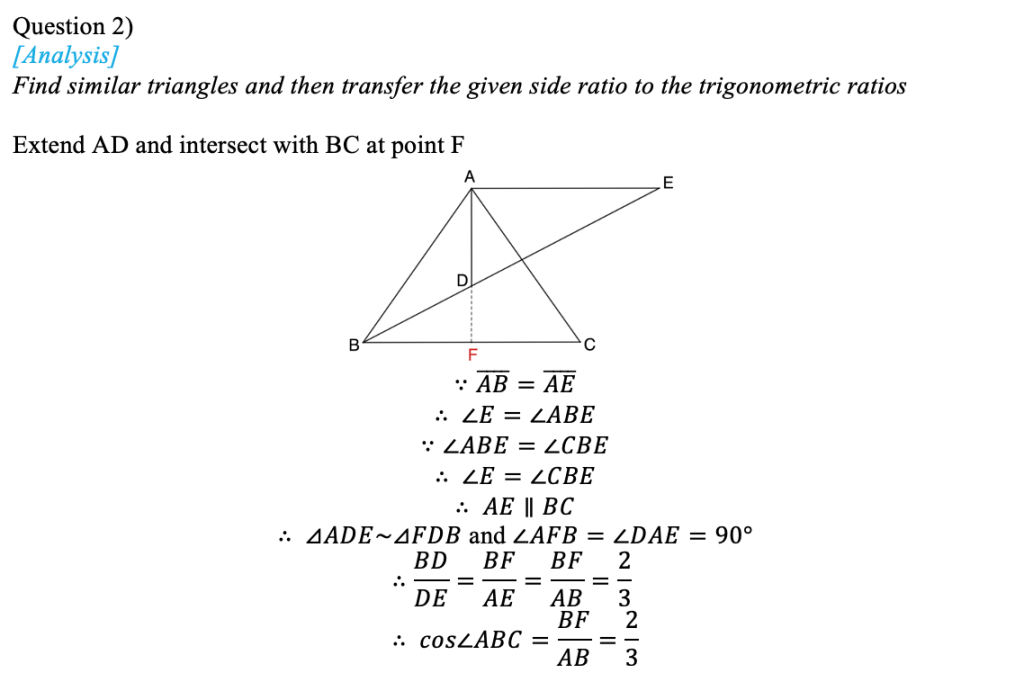
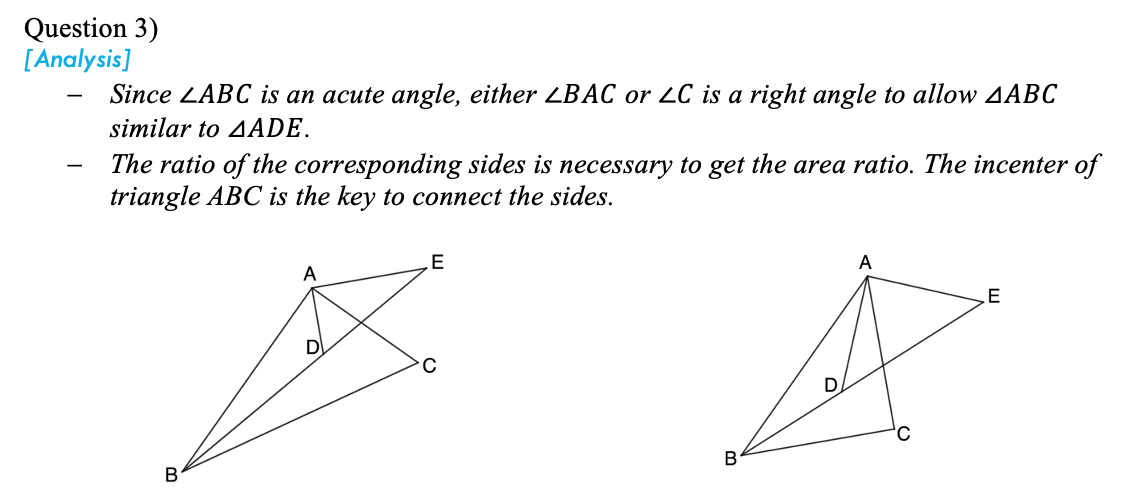
The three questions cover many contents, such as angle bisector, special trigonometric ratio, similar triangle and triangle incenter. Question 3) is challengeable in two ways. Firstly, there should be two cases according to the given information. Secondly, none of the side length is given but is needed to get the area ratio of the two similar triangles. The key to find the side ratio lies in the special right triangle 30-60-90 degrees and 45-45-90 degrees. Besides, the property of the incenter is the adhesive of the sides in two similar triangles
Students’ performance on the test
According to the Municipal Education Commission, the difficulty of the test paper is originally designed into 3 levels, 80% easy, 10% medium and 10% hard. As the full mark of the test is 150 points, 80% easy means that most students can secure a score of 120. Table 2 shows the statistics of students’ performance in Math Proficiency Test in 2018 and 2019. If students get 130 (roughly the median of each year) on the Shanghai Middle School Math Proficiency Test, they should have mastered the basic concepts and skills such as solving rational equations, simplifying algebraic expressions with exponential, radical and/or rational expressions, able to solve easy to medium level functions and geometry and so on. Please note that the level of difficulty is defined by the Chinese education system. Only by finishing the test paper in 100min can one explicitly understand the distribution of difficulty.
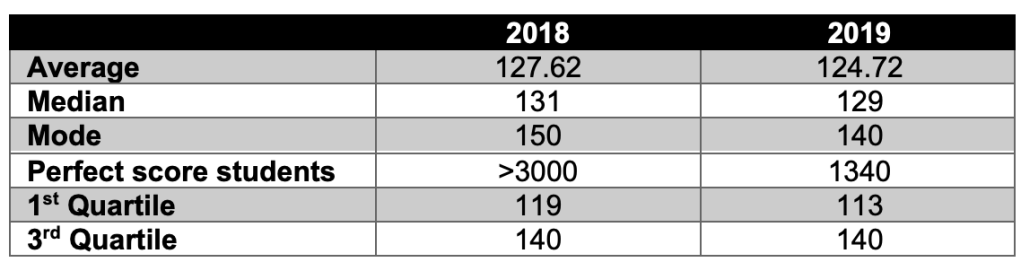
Here, we also need to look into the high school acceptance rate to understand the competency of the test. In the past ten years, the average high school acceptance rate is around 55% to 65% with some slight fluctuations year by year. However, only about 25% of the students can be admitted into municipal key high schools which will almost guarantee a ticket to a university three years later. To be the top 25% on the whole, students are most likely to be top 25% in math as well. The third quartile reveals that students should reach 140 or higher, losing 10 points top. To get 140 or more on the test, mastery of the basic concepts and skills are far from enough. Usually, quadratic functions and geometry proof are the main parts setting students apart from median to top. To succeed in the 10% hard questions of functions and geometry, students need to have strong
- logic thinking
- forward and reverse reasoning
- comprehensive and complete thoughts
- imagination of transformation in space (refer to the example questions 24 and 25).
Truly, these abilities are similar to, or to some extent more challenging than, the corresponding content of IB DP higher level mathematics, or AMC 8/10, but are imposed on the 15-year-olds in Shanghai. Indeed, extraordinary abilities are necessary to stand out of such a huge population.
Bibliography
[1] PISA 2018 Results (Volume I): What Students Know and Can Do. P48
[2] http://www.shmeea.edu.cn/page/03500/index.html