Drawing from my decade-long experience as a math teacher, I’ve observed that the introduction of geometric proof often marks a fresh beginning for middle school students. Interestingly, students who are good at algebra may not necessarily excel in geometry, while those under performers in elementry school may surprisingly develop a fondness for geometry. In contrast to school algebra, geometry presents distinct cognitive challenges mainly involving spatial reasoning and deductive reasoning. The process of solving high-cognitive geometric questions often mirrors the thinking patterns mathematicians experience. During the process of problem solving, intuition is considered of great importance to mathematicians (Burton, 1999). Similarly, intuition also plays a pivotal role in solving challenging geometric problems, especially when the application of auxiliary lines is essential. However, intuition is not an innate trait; rather, intuition is built upon a foundation of prior knowledge, attempts and thought (Schoenfeld, 1982). Therefore, intuition is a skill that can be nurtured and developed over time. Through exposure to various mathematical concepts, problem-solving scenarios, and real-world applications, individuals gradually cultivate the ability to perceive patterns, make informed guesses, and formulate conjectures. The teaching and learning of geometry in Chinese middle schools appear to offer a platform for unveiling the enigmatic nature of intuition.
Geometry curriculum of Shanghai Middle schools
Geometry education holds a pivotal role within the mathematics curriculum of Chinese middle schools. Its significance is underscored by the fact that geometry constitutes 40% of the High School Entrance Exam. To excel in the selective exam, students undergo rigorous and intensive long-term training. From 7th to 9th grade in China (i.e., Shanghai), students delve into the realm of geometric proofs, exploring concepts such as parallel lines, congruent triangles, parallelograms, rectangles, squares, rhombi, similar triangles, and circles. Table 1 provides an overview of the geometry-focused curriculum in Shanghai’s middle schools, with sections highlighted in blue denoting topics involving geometric proof. In a typical public middle school, math classes are given daily and there are about seven 40-min math classes each week. In addition to taking math classes, students also do homework to reinforce their grasp of the daily lessons everyday. In fact, many schools and math teachers spend more time on instruction to achieve the teaching tasks.

Aligned with the van Hiele Model of Geometric Thinking, Shanghai middle school students are expected to attain Level 3 Deduction, which is a prerequisite for success in the High School Entrance Examination. For instance, the majority of students are expected to successfully solve the first two sub-questions presented in Figure 1, however, only a small part of students can handle the last sub-question. The challenging nature is not confined to this selective middle school graduation examination, but is reflected in the difficulty of practice questions encountered throughout the three-year period. A notable strategy employed to tackle these cognitively demanding problems involves the strategic utilization of auxiliary lines.

Teaching and learning of auxiliary lines in school
The strategic placement of auxiliary lines, often guided by deductive reasoning, forms a crucial aspect of geometric problem-solving. Chinese educators distill these auxiliary line techniques into practical rules that students apply extensively through focused practice to attain mastery. For example, when a midpoint is given, a congruent triangle can be constructed by extending the line bisecting the midpoint. Figure 2 demonstrates two methods of adding auxiliary lines involving midpoints to solve the last sub-question of question 25. The congruent triangle acts as a link to unveil hidden information within the problem. While various methods for incorporating auxiliary lines exist, for instance, extending line BG to intersect line AC exemplifies an alternative strategy, the utilization of lines related to midpoints often presents a promising approach to uncover additional conditions conducive to proving a given statement.
Various other techniques are employed as well, including extending lines to create intersections, establishing parallel lines, introducing triangle heights, and utilizing transformations such as reflection, rotation, and dilation. These rules serve as a foundation, accompanied by comprehensive practice enabling students to adeptly employ them in resolving analogous problems. While these rules are advantageous for handling similar problems, they offer limited assistance in navigating intricate, comprehensive, and high-cognitive ones. To solve the challenging novice problems, students must often engage in authentic mathematical activities akin to mathematicians (Stylianides, 2022), involving a movement between conjecturing, refutation, and constructing coherent arguments.
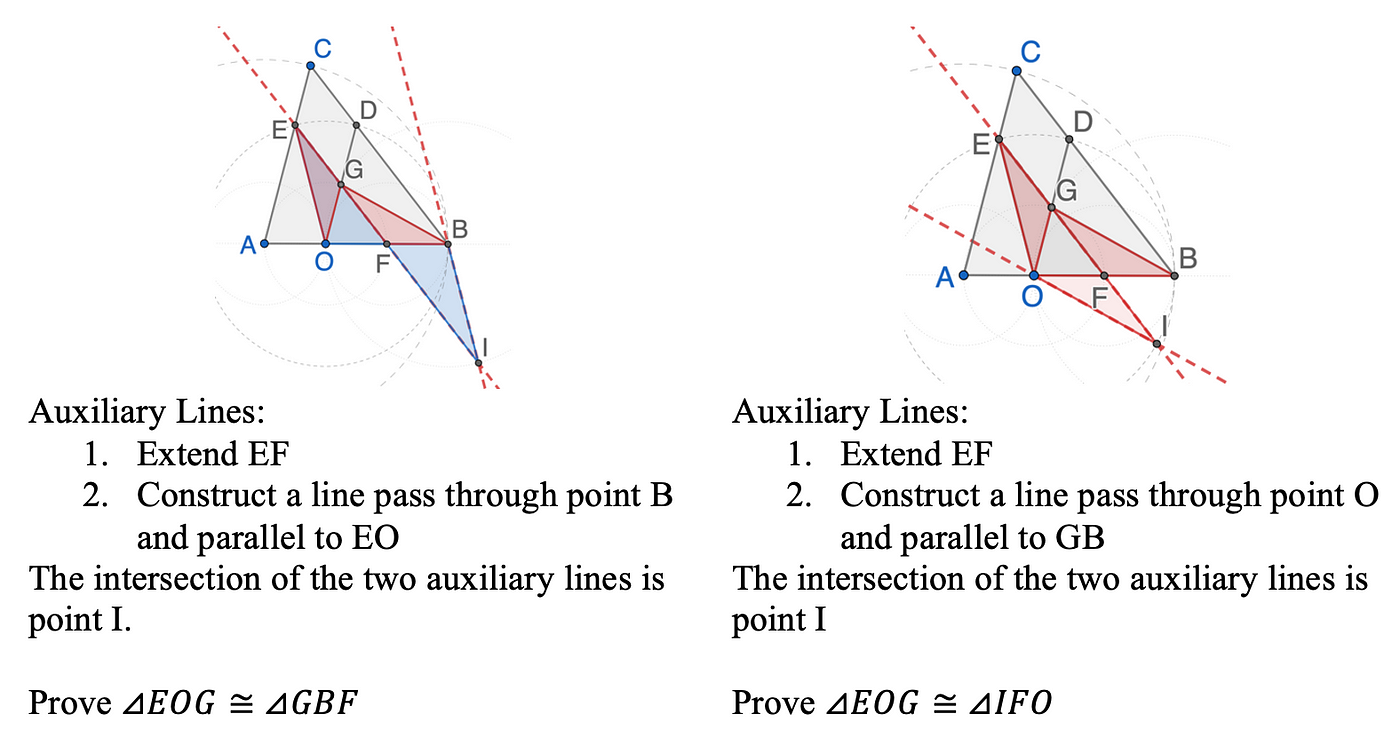
Students’ growth through learning geometric proof
Most students experience a hard transition from Algebra to Geometry in the second semester of Grade 7. Unlike equations or area calculations, geometric proofs require students to demonstrate the validity of a given proposition, a task that initially brings about discomfort. In Shanghai middle schools, geometric proofs starts with identifying parallel lines, which serves as a relatively straightforward introduction. However, despite its apparent simplicity, students spend morethan an hour on homework involving two or three moderately complex geometric proof questions. The composition of proofs and the application of logical reasoning present novel challenges that requires considerable time and effort to become adapted. Congruent triangles are taught right after parallel lines. With some experience, students begin to comprehend the formal structure of geometric proofs. Nevertheless, as they confront more cognitively demanding problems, they struggle a lot more, not in the format of writing but in figuring out the hidden information necessary for solving the problem. On average, when faced with challenging questions, students invest 1.5 to 2 hours in their homework, sometimes even without arriving at a resolution. However, the positive part of this practice struggling is that it fosters substantial growth in deductive reasoning skill and perseverance. In the eighth grade, concepts such as right triangles, angle bisectors, and quadrilaterals come into focus. Students become less anxious about challenging questions, striving to employ strategies imparted in class to solve intricate problems. With considerable and consistent effort on problems necessitating numerous reasoning steps and the consideration of diverse scenarios, students advance to the rigorous nature of geometric proofs. This process of proving can be described as “Lakastos-style proving” (Komatsu & Jones, 2019), which demonstrates repetitive trial-and-error in exploration of conjecture and arguments. Grade 9, the last year of middle school, covers the two most demanding topics: similar triangles and circles. Students commit themselves diligently to memorizing strategies, practicing consistently, and reflecting on their progress. The culmination of intensive and protracted training equips most students to master theorems comprehensively, accumulating a wealth of experiential knowledge in preparation for the examination.
Discussion 1: Intuition can be cultivated
In my article “Is A Head Start Helpful in Geometric Proof and Deductive Reasoning?”, I describe two learning paths of students in my honor math class: rote memorization and deductive reasoning. Students prefer rote memorization rely heavily in worked out examples initially, remembering that midpoints imply extending the line segment bisecting the midpoint; students apply deductive reasoning advance through metacognitive practice, bridging the gap between conjectures and evidence. Mevarech 2003 indicates that the effect of metacognitive training outperforms that of worked-out examples on students’ mathematical reasoning. My conclusion that a head start is not help in deductive reasoning aligns with his observation but through an alternative perspective. However, when considering students’ overall progress and, more specifically, their development of intuitive abilities to tackle challenging questions, both groups of students exhibited noticeable advancements in deductive reasoning over the course of the three-year study. This underscores that intuition is indeed cultivable. While the paths taken by different students may vary, the common thread lies in educators’ ability to foster an environment conducive to cultivating intuition. Surely, the exam-oriented Chinese educational system has its own drawbacks. Educators should look for more efficient ways to improve students deductive reasoning abilities, such as encouraging students to engage in exploratory thinking and profound metacognitive training.
Discussion 2: Is there a limit?
I can often hear G6er’s and G7er’s parents say, “My child doesn’t work hard enough. If he also works as hard as A, he will be as good as A.” The answer usually emerges vividly in Grade 8 when most students realize the importance of the High School Entrance Examination and work hard to prepare for it. Many of those parents realize that learning outcomes can vary significantly even with similar amounts of practice. Innate abilities including intelligence and creativity do play a role (Meier, 2022), but the Chinese geometry education proves that dedication, perseverance, and targeted training can push those limits further. Yet, reflecting on my own experience with the 2023 International Olympiad Mathematics, it seems that I don’t possess the intuition to solve these exceedingly challenging questions. Can I transcend them? Could professional training and the accumulation of substantial experience enable me to overcome these boundaries? If I can indeed surpass these constraints, where is my next limit? Are there certain limits that remain impervious to improvement, irrespective of the strategies applied to individual students? How can teachers stimulate students’ potentials to the greatest extent?
Reference
Burton, L. (1999). Why Is Intuition so Important to Mathematicians but Missing from Mathematics Education? For the Learning of Mathematics, 19(3), 27–32. http://www.jstor.org/stable/40248307
Komatsu, K., & Jones, K. (2018). Task design principles for heuristic refutation in Dynamic Geometry Environments. International Journal of Science and Mathematics Education, 17(4), 801–824. https://doi.org/10.1007/s10763-018-9892-0
Meier, M. A., & Grabner, R. H. (2022). The roles of Intelligence and Creativity for Learning Mathematics. Handbook of Cognitive Mathematics, 648–679. https://doi.org/10.1007/978-3-030-44982-7_6-1
Mevarech, Z. R., & Kramarski, B. (2003). The effects of metacognitive training versus worked-out examples on students’ mathematical reasoning. British Journal of Educational Psychology, 73(4), 449–471. https://doi.org/10.1348/000709903322591181
Schoenfeld, A. H. (1982). Some thoughts on problem-solving research and mathematics education. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 27–37). Philadelphia: Franklin Institute Press.
Stylianides, A. J., Komatsu, K., Weber, K., & Stylianides, G. J. (2022). Teaching and learning authentic mathematics: The case of proving. Handbook of Cognitive Mathematics, 727–761. https://doi.org/10.1007/978-3-031-03945-4_9
Leave a Reply