Question: Suppose a convex polygon has exactly 4 obtuse interior angles. What is the maximum number of the sides of such a polygon?

Hints behind the information

1. Convex polygon？A polygon with all its interior angles less than 180°
2. exactly 4 obtuse interior angles: 90°<obtuse angle<180° (Hint: the other interior anlges ≤ 90°) 
3. maximum number of the sides? What’s the relationship between sides and interior angles?

Let’s use regular polygons to explore as all the regular polygons are convex polygons.

Visual Observation: sides and interior angles

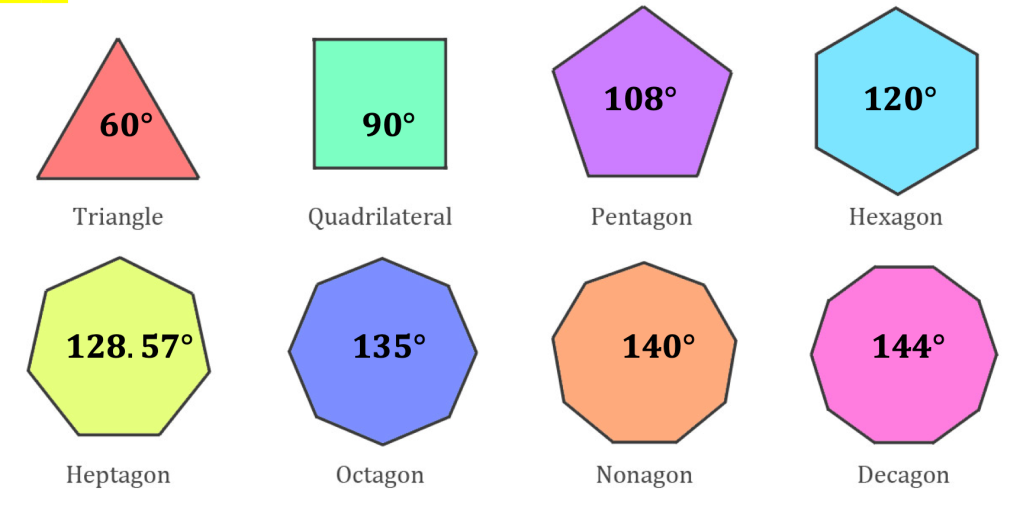
Observation 1:

• The More the sides, the Greater the interior angles.
• The Greater the interior angles, the More the sides.
• The number of sides is the same as the number interior angles.

Observation 2:

• If there are 4 right angles, it is a rectangle.
• This indicates that when there are more than 4 sides, there are 3 right angles at most.(refer to the graph above, by cutting a right angle, there are 3 right angles left and the polygon turns from a square into a pentagon.)

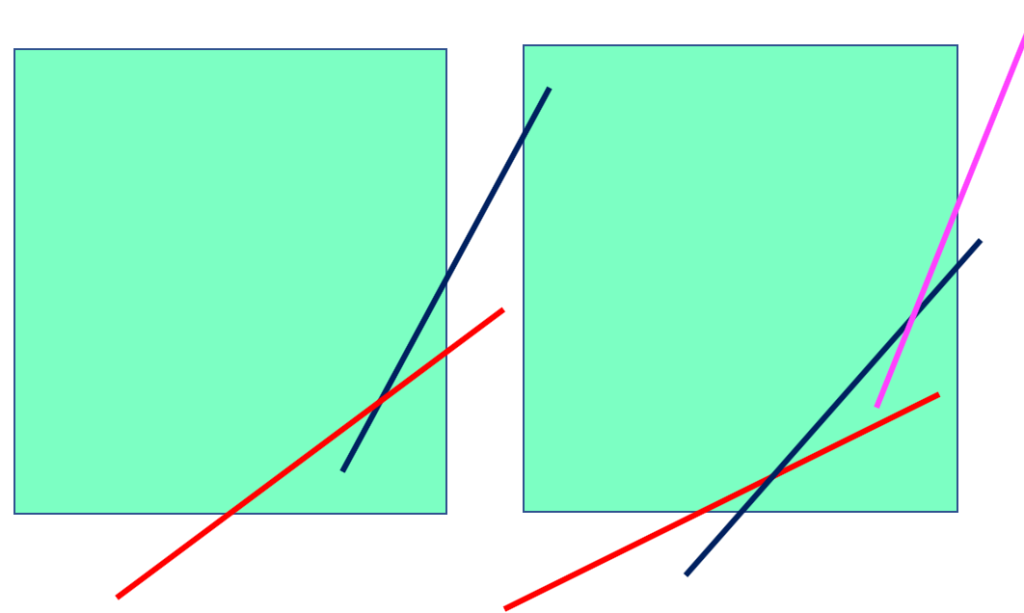
Observation 3:

• Based on “Observation 1” and the graphs above, if there are 3 right angles, the more the sides, the greater the interior angles.

Conclusion about sides and interior angles:

So far, we can conclude that to get the maximum number of sides, the interior angles should be as great as possible.

Combine the conclusion & information：

• exactly 4 obtuse interior angles: All the other angles = 90° allow for the maximum number of sides.
• There are 3 right angles at most for a polygon with more than 4 sides.

4 obtuse angles + 3 right angles = 7 angels –> 7 sides

---

Use formula and inequality  

The sum of interior angles = (n-2)∙180°

This sum should be less than the sum under the maximum situation. But what is the maximum situation?

exactly 4 obtuse interior angles implies:

• the sum of the 4 obtuse angles < 4∙180° (all angles in a polygon is less than 180°)
• the sum of the other angles ≤ (n-4)∙90° (the other angles are either acute angles or right angles, a maximum situation occurs when all the other angles are 90°. )

Inequality: Sum < the maximum situation

• (n-2)∙180° < 4∙180°+(n-4)∙90°
• n < 8
• So, n(max)=7

This polygon has 7 sides at most. It can be a heptagon. 

---

Test your evolution

A convex polygon with 4n+2 sides can be expressed as A₁A₂A₃—A_(4n+2). If each interior angle is a multiple of 30 degrees and∠𝐴₁=∠𝐴₂=∠𝐴₃=90°, find the value of n.

Can you use the above-mentioned methods to solve this question?